Introduction to Modern Cryptography.
Hi, so i decided that, as i have the entire week to my self i will put in an introduction to
Cryptography, for all who are interested in the subject. I will be updating the post, for the next week, with new information and sections on cryptography.
Ok, before we move into the real interesting subjects of cryptography like, key exchange protocols, signatures, certificates, Symmetrical cryptography and Asymmetrical cryptography, hash fictions, and prime numbers. We will first look into the history of cryptography and its origins,
History of the Hidden Language. During ancient times, when leaders and generals needed to send messages to their troops, with instructions on what they should do. It was very easy for the enemy to intercept those messages , by ambushing supply routs (in modern time its equivalent is the man in the middle attack), So this meant the message was easily read and the enemy would know what the other side was planning. to prevent this from happening there was only two ways of preventing this from happening, First, was to hide the message so that it looks just like a normal every day thing (
Steganography). Steganography the art of hiding messages so that it is only known to the person receiving the message that a message is hidden in it, a good example is invisible ink. Now, the Second way was to make the message unreadable for any person, who was not the intended recipient. And this is what many did, because unlike stenography encryption could be taught to people easily and could be done with much less resources. so In a war situation teaching generals and messengers how to implement cryptography was much more efficient.
Early encryption techniques were rather simple and you yourself may have played with it when you were kids.
Two main cipher system used were. Transposition cipher
Substitution ciphersA
Transposition cipher uses a very simple method of encryption one of the most popular ones were the
scytale, basically the scytale is a piece of wood, on which a strip of paper is wounded up to revel what the message is. So the person sending the message to some one would have an identical scytale as the other and would wind the paper on it and write the message then, unwind the paper and fill the empty space with random words. if another person intercepted the message and used a different size scytale the message would not show.
Problem with this was the sender and the receiver required identical scytale.
A Scytale 
A
Substitution ciphers is another simple cipher that substituted the actual alphabets with some other alphabets or numbers. The
Caesar Cipher is by far the most famous of them all, used a simple shift technique to substitute the alphabets, Used by
Caesar himself and the roman empire Eg bellow.
Three shift right
→Plain: A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Cipher: X Y Z A B C D E F G H I J K L M N O P Q R S T U V W
Planetext - Bitcoin is a crypto coin
Ciphertext- Efqzlfk fp x fovmql flfk
Notice there is repetition of the same alphabets that have been substituted .
So, looking at the cipher above you can now encrypt any length of message through substitution, and all the receiver has to know when receiving the message is how many shifts are used.
However all these methods are venerable to
cryptanalysis techniques, like a
frequency analysis. All a person has to do is count the alphabets and make a note of each of the alphabets and the number of times it appears. In the english language some alphabets appear more that some, using this, we can determine which symbol or alphabet was replaced .
Frequency graph
 Polyalphabetic cipher
Polyalphabetic cipherDue to the ease of all these Cipher being broken a new system was requires, one which could not be so easily broken using a frequency analysis. many new ciphers came in and out. One being predominantly used for hundreds of years was the
Polyalphabetic cipher on which normal frequency analysis attack method did not work. and it used a key. The
Vigenère cipher the best known of them all and its harder cousin Autokey cipher remained one of the most used ciphers during the 15th and the 16th and up to mid 18th century, remained unbroken.
It was a variant of a Substitution ciphers but with multiple shifts and alphabets and also the use of a key made it versatile and impenetrable.
This is how a Vigenère cipher looks like.
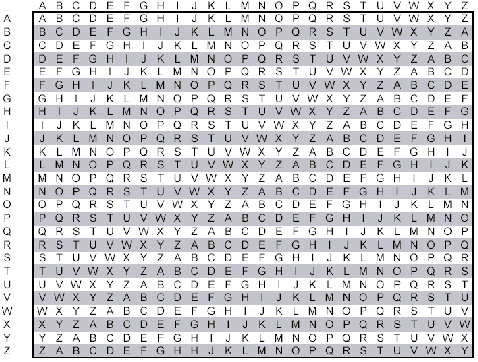
Eg:-
Message - TO BE OR NOT TO BE THAT IS THE QUESTION
KEY - RELATIONS
Keyword: RELAT IONSR ELATI ONSRE LATIO NSREL
Plaintext: TOBEO RNOTT OBETH ATIST HEQUE STION
Ciphertext: KSMEH ZBBLK SMEMP OGAJX SEJCS FLZSY
Notice there is no repetition of the same alphabets that have been substituted .
This kind of ciphers remained active for many hundreds of years and was used widely in Europe and the middle east. However the fate of this cipher system was doomed, when a brilliant man who we all know and admire in the computing world came along, the father of computer Charles Babbage, he broke both the Vigenère cipher and the much harder Autokey cipher.
Tomorrow we will touch upon mechanical ciphers, used in the second world war and then, enter the world of modern cryptography in the digital age.
_______________________________________________________________________________ ________________
Section 2The Rise of the Machine The era of the
Second world war, was the proving grounds for modern encryption methods, ideas and innovation. In my opinion, if it was not for the Mathematicians,
code-breakers and revolutionary thinkers, the modern computer age, the internet and space travel would not have been possible at all. The birth of computing devices, to conduct tasks through programmed inputs were all tested and innovated, by codebreakers trying to break the German Enigma code. The use of early
computers was at England, in a place called
Bletchley park. In fact, the first discovery of modern public key encryption system and early experiments on One Time Pads was done during this time.


Enigma Machine *Germany*(
Left) SIGABA *USA* (
Middle) TypeX *UK*(
Right)
During the War the Germans used one of the most successful, mechanical crypto systems called the
Enegma machine, it was a
rotor cipher machine, similar to a Polyalphabetic cipher but with the difficulty increased by the rotor, if the allies broke the code, all the germans did was change the configuration and may be add rotors giving another huge headache for code-breakers.
The US and the UK also used similar machine called the
SIGABA and the
TypeX. However, a code system that was never broken by the enemy was not mechanical at all, but were the
Navajo code talkers who played a vital role in the success in the pacific war theater . There's even a movie called the Windtalkers played by Nicolas Cage although it concentrated more on the nipless cage than the
Code talker.
 Modern Cryptography
Modern Cryptography With progress happening in the Cryptography community, one of them was by far the most revolutionary, the
public key crypto system, the
RSA algorithm allowed people to have two keys, one public and one private. this solved many problems of key transfer, security and validity of a encrypted message. This algorithm was made during the second world war, but was classified. Until 1977 when a group in
MIT rediscovered this algorithm on their own, hence the name RSA algorithm, the first alphabet of their surname
Ron Rivest,
Adi Shamir, and
Leonard Adleman.
The advent of modern cryptography gave rise to secure communication, safe banking transaction, and greater communication, and social revolution. We use some form of encryption every day and sometimes we don’t even know that encryption is being used.
Cryptography, before the dawn of the Information age was confined to the intelligence community, with many of the technology kept classified and inaccessible to the general public. It was nearly impossible for a person without a connection to the intelligence community, or a large corporation like IBM to do any work on Cryptography. But, that all changed when the internet was born. People from around the world collaborated to bring cryptography to the masses. With the advent of the internet people were able to disseminate information about cryptography, and develop software for everyone to use.
This shift in knowledge from an intelligence based community to a worldwide public community, gave rise to many social changes. With people openly advocating the use of encryption to promote privacy, Bring down corrupt government, safeguard whistleblowers. During the late 80's many BBS's hosted score of text files relating to cryptography and around the early 90's a cypher punk mailing list was started, the birthplace of the cyberpunks, with the major discussion on technical issues, alternative uses of cryptography privacy, government surveillance, freedom of speech, civil society, and related issues. There have been many influential individual who have shaped this movement Eric Hughes, Jim Bell, Philip Zimmermann, Julian Assange just to name a few.
The roots of bitcoin can be traced back to the early discussion, within the cyberpunks and the cryptoanarchistic groups for an anonymous banking system. May be Satoshi Nakamoto might be one of the early cypherpunks, who was able to solve the problem of anonymous banking. But, we shall never know.
Cryptography has now become an integral part of our lives, in this modern day society it is rare not to come across technology that does not utilize some sort of encryption. I believe that the future for Cryptography is bright, because this is the only thing that can solve many of the world problems of secure communication, Tyrannical governments, greedy Banks, and immoral super corporations. What the future holds for cryptography is can only be speculated, with
quantum computers in the forefront of computing technology, it might as well be foretold that computers are gona be far more smaller, powerful, and consuming less power.
Just imagine the next Bitcion Hashing arms race with people using
Q-chips. instead of the outdated ASIC's, the Q-chips able to do 1,000 times more processing than the ASIC's. A hundred time less power. But, Q-chips are still a few years away so ASICS are still gona be active . Ok now i'm moving away from topic, so let me stop my self there.
Tomorrow we shall finally talk about the technical part of modern Cryptography. Thinking about what to talk about tomorrow . I am a bit torn about where to start this from, and after a cigarette break I have decided to start with the basis of modern cryptography, the math’s behind it, so the topic for tomorrow would be
Prime number related math’s, and will touch upon a
Diffie and Hellman key exchange protocol .
_______________________________________________________________________________ ________________
Section 3The Numbers Game The building blocks of every thing in maths my opinion is and always, the prime number. This number can form so many different numbers of any length, and a number of a particulate digit can be factorized to a smallest number being prime.
What is a prime number? A
prime number is a number divisible by it self and one. (basic old school definition)
take it this way, a number which cannot be divided equally without creating fractions of it.
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71...............so, lets take for example an integer which Factorizes to
56984 = 2 × 2 × 2 × 17 × 419what is prime factorization? Prime factors of a positive integer are the prime numbers that divide that integer exactly like the example above.
so why is this useful to cryptography and online security? Well the simple fact is that, it is easy to multiply two large prime numbers, but while trying to find the prime factor of that integer become a tedious task taking alot of time
a simple example like.
7703 × 6421 = 49460963
the output a compost number is going to take a long time to be factored, the example above may not be the best example of a large prime number being used but just Imagine a prime number P1 and P2 both the length of about 100 digits long or much longer and multiply those tow together the composite number would be hard to factorize the limit being the time taken to compute the result.
g mod p
42 mod 12 = 10Working with prime modulus.
3^29 mod 17 = 12so here calculating this makes it easy when we have the generator as 3 raised to the power 29 . However when we have the result as 12 and need to find 3 raised to the power x . this becomes a time consuming task.
3^x mod 17 = 12This problem is also know as a
discrete logarithm problem. Therefor this creates a One way function. easy to compute harder to decipher.
Therefore, if the size of the prime increases the time taken for a computer to compute the result of that, would take a very long time.
Clock arithmetic :
If we consider prime numbers as the ingredients in our encryption recipe, the
modular arithmetic is utensil for cooking it up. we shall see a simple use of [ mod ] in a few examples while talking about the Key exchange protocol especially the Diffie and Hellman key exchange protocol.
Diffie and Hellman key exchange protocolProblem of Exchanging Keys :-
Lets take an example of two people who are honest employees in a corrupt government service,
Alice and
Bob, and lets take for example their
Evil boss is
Eve.
Alice and
Bob want to communicate with each other but, does not want any one to read their messages, as they know Eve would most likely be reading their emails.
so how would the two communicate without
Eve being able to read their messages.
Firstly, Alice and Bob has to agree on a
secret key so that they can use that key to encrypt messages and send to each other.
but, the problem is that if they send the key without encrypting it , Eve would know what the key is and can read all the messages Alice and bob send each other.
This is where the
Diffie and Hellman key exchange protocol would be most usefull.
So how does it work?
Eve ('g' & 'p') ↑
Alice and Bob agree on a generator and a prime modulus. Alice ← 'g' & 'p' → Bob
g = 3
p = 17What Alice does :-
She chose a random number Alice (x) 'Private number'
x=54and then raises that on the generator, result q = 15
g^x mod p = q Eve ('g','p' & 'q')3^54 mod 17 = 15 ↑
Alice 'q' → Bob
Alice, then sends this result 15 over the insecure line to Bob
What Bob does
He chose a random number Bob (y) 'Private number'
y= 24and then raises that on the generator, result r = 16
g^y mod p = r Eve ('g','p','q' & 'r')3^24 mod 17 = 16 ↑
Bob 'r' → Alice
Bob, then sends this result 16 over the insecure line to Alice
What Alice does is,
uses Bob's result as a generator raised to the power of the random number Alice chose to calculate a secret key s
r^x mod p = s16^54 mod 17 = 1Bob also does the same thing using the number Alice sent Bob. to generate a secret key s
q^y mod = p = s 15^24 mod 17 = 1Here Both
Bob and
Alice was able to compute the
secret key s without transmitting the key over the insure line.
Meanwhile,
Eve who is reading the messages coming in, can only intercept the following details from Bob and Alice
the generator 'g', prime modulus 'p' and the two results of the calculation by Alice and Bob 'q' and 'r'.
What Eve is missing is the private numbers that Alice and Bob used to generate the Secret 's' . without the 'x' and 'y', it is impossible for Eve to determine what secret key Alice and Bob is using to encrypt their messages.
Alice '(m)' → Bob s(m) s(m)
So, here Alice sends Bob an encrypted message using a secret key 's', which Bob then uses the Secret key 's' to decrypt the message Alice Sent him.
As you can see with this protocol many of the problems of secret key transfer is solved. This also leads us to the path of asymmetrical encryption and the use of the later RSA algorithm's public key cryptosystem to encrypt messages.
I hope this was simple to understand, i tried to put in as much details without making it confusing, i hope you all like it and understand. Next, i will cover the public key cryptosystem namely the RSA algorithm, and then touch upon Hashing, one time pads and a few single key encryption on block ciphers.
_______________________________________________________________________________ ________________
Section 4Asymmetrical Cryptosystem The problem faced with cryptography is that when two parties area involved a predetermined key is required. This creates a problem of compromising the key. the other problem is that, if the two people are not able to meet and set a key they would obviously need to communicate the key agreement using the Diffie and Hellman key exchange protocol. Communication between the two people may not be a viable option, and even dangerous. In this case the most easiest Crypto system would be the use of a double key encryption/ public Key Cryptography.
A public Key cryptography can serve two different purpose First and the foremost is encrypting messages. Secondly, for signing messages and providing authenticity.
A public key cryptosystem is built in two parts the first part the private key or the secret key, second is the public key, by it name you know that it is to be public and can be openly distributed to any on or even published in public. But, not the private key, the private key stays with the user and should be kept as safe and not shown to any one.
The principles of Public key cryptography plays a pivotal role in the Bitcoin ecosystem. The Bitcoin address that is generated, is part of a public key. the public address you see of a Bitcoin is a hashed key of a ECC(Elliptic Curve Cryptography) pair. Infact it uses a ECDSA (Elliptic Curve Digital Signature Algorithm) public/private key pair, then it is processed through a SHA-256 hash till a base 58 format is created which is the Bitcoin public address.
For now we shall study the use of the RSA algorithm, rather than the ECC(i'm a bit rusty with the ECC

)
Alright, Let us take Alice and Bob, two lovers we are desperately wanting to communicate with each other, but they are kept apart for each other by their family, who are rivals in the spice trade. Both the families are able to intercept any communications between Alice and Bob. and Eve is the one reading all the messages.
OK, Alice and Bob now creates a public key pair on their own.
Alice and Bob chose two separate prime numbers p1,p2.
The they Take p1,p2 and multily to get n.
p1*p2 = n | Alice | Bob |
| p1 | 53 | 61 |
| p2 | 59 | 53 |
| n | 3127 | 3233 |
Now both of them chose 'e' such that 1 < e < φ(n)
where in φ(n) is, φ(n) = φ(p)φ(q) = (p − 1)(q − 1), a Euler's function
being φ phi .
Public Key Now, e is what is assigned as public key. so For Alice the public key is = 3 and Bob is = 17
We not go and calculate the private key 'd' for both Alice and Bob.
being,
d = (K*φ(n)+1)/(e)d is the multiplicative inverse of e (modulo φ(n))
So after computing d we get :
Private Key So now both Alice and Bob has their public and private key .
| | | Alice | Bob |
| Private Key | d | 2011 | 2753 |
| Public Key | e | 3 | 17 |
Alice Publishes the Public key and 'n' on the news paper public key = 3, n= 3127 (or may be some thing more discreet like " My favorite number is 3" )
Bob Publishes the Public key and 'n' on the news paper public key = 17, n= 3233(or may be some thing more discreet like " My favorite number is 17" )
Eve can see both the key's.
Encryption : - Bob sends a love letter to Alice.
c = m^e (mod n) (using the public key of alice)
So lets take for example the message 'm' is 89
89^3 (mod 3127) = 1394therefore c= 1394, this becomes the encrypted message
Eve |
Bob --> --c 1394--->^----->
AliceEve has the message now but cant understand any thing she would need Alice's Private key in order to know the content of the message.
Meanwhile, In the safety of her room Alice get the encrypted message, she goes over to her safe and gets her private key to decrypt the message.
Decryption becomes fairly simple when the private key is known .
m=c^d(mod n)there for the message 'm' is
1394^2011 (mod 3127) = 89Here the prime factorization of 'n' becomes crucial, if the prime numbers used are of a long length the time factor for calculating the prime factor become impossibly long and tedious. so the main protection in a public key cryptosystem is the calculation time required to find the prime factor. longer the prime numbers used longer for the computers to compute the prime factor.
Now, we shall look into digital signature. A digital signature is a way of proving a persons authenticity,
What a person does is takes his private key encrypts a message and sends it to another person .
So for eg. Alice wants to send a legal document to Bob, but Bob is scared that some one may intercept the message and send a false document to him . so for Bob to know if the message is from Alice it needs to have some type of verification.
So Alice takes a document and encrypts it using her Private Key and sends it to Bob.
Bob then uses Alice's public key and decrypts it, if it decrypts then the document is from Alice if it does not then the message may be compromised and not verified.
Here the process is in reverse. it is only used to provide identity of the sender. the message can be digitally signed using the senders private key and encrypted using the recipient's public key.
Ok that covers most of public key encryption and signature using RSA, i will be following up on later editions, do suggest what you would like to see and do ask me any questions, i will answer.



