|
Raystonn (OP)
|
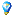 |
June 17, 2014, 04:00:50 PM
Last edit: September 09, 2014, 04:32:42 AM by Raystonn |
|
We have now hit an all time high for Bitcoin adoption, and it looks to continue its upward trend. As you can see, Bitcoin's price is heavily correlated with the Metcalfe's Law value of Unique Addresses ^2. I see no signs of this correlation changing, nor of adoption slowing. This implies a continuation of the exponential rise in Bitcoin's price. Sometimes adoption leads price, and sometimes price leads adoption. You can see this if you analyze the long-term trend in the top chart. At this point it looks like adoption is going to lead price.  Here is the chart zoomed into the right side of the chart for better analysis:  Edit: Updated 9/8/2014 with latest data. |
|
|
|
|
|
Raystonn (OP)
|
 |
June 17, 2014, 09:48:20 PM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
|
|
|
|
|
|
BuildTheFuture
|
 |
June 17, 2014, 10:10:21 PM |
|
Sounds good, I'm hoping services like Circle (if they ever send me that invite I requested) will help quite a bit with mainstream adoption. Just speaking as a consumer, if I can buy bitcoin without fees and spend it at merchants that provide a better discount than my credit cards' 1% reward points, then I'll ditch the cards and switch to bitcoin and gift cards bought with bitcoin. I'm sure there are a ton of people out there who would also switch if they start seeing these discounts pop up.
|
|
|
|
|
Torque
Legendary

 Offline Offline
Activity: 3822
Merit: 5504

|
 |
June 17, 2014, 10:25:51 PM |
|
Just speaking as a consumer, if I can buy bitcoin without fees and spend it at merchants that provide a better discount than my credit cards' 1% reward points
This and this. If these two things happen, then the late adopter mass consumers will eventually get won over. If not, then it's doubtful, sadly. Today bitcoin still remains a very inconvenient and costly way to pay for shit. |
|
|
|
|
|
BTCfan1
|
 |
June 17, 2014, 10:54:58 PM |
|
can you explain metcalfe?
|
|
|
|
|
|
Raystonn (OP)
|
 |
June 17, 2014, 11:06:18 PM |
|
|
|
|
|
|
|
Wary
|
 |
June 18, 2014, 05:06:28 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
It's an illusion. S curve has no vertical stage, just like an exponential curve doesn't have it. The rate of adoption is already (and had always been) exponential, that's why it looks like straight line on the log-scale chart. |
Fairplay medal of dnaleor's trading simulator. 
|
|
|
|
Raystonn (OP)
|
 |
June 18, 2014, 05:10:29 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
It's an illusion. S curve has no vertical stage, just like an exponential curve doesn't have it. The rate of adoption is already (and had always been) exponential, that's why it looks like straight line on the log-scale chart. No. The rate of adoption is currently linear. The Metcalfe value is exponential. That is the number of unique addresses used per day, squared. Vertical is an expression. The middle of an S curve looks nearly vertical. |
|
|
|
|
|
Wary
|
 |
June 18, 2014, 05:15:07 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
It's an illusion. S curve has no vertical stage, just like an exponential curve doesn't have it. The rate of adoption is already (and had always been) exponential, that's why it looks like straight line on the log-scale chart. No. The rate of adoption is currently linear. The Metcalfe value is exponential. That is the number of unique addresses used per day, squared. Vertical is an expression. The middle of an S curve looks nearly vertical. Look at left side of the OP chart: it is in log scale. Curve that looks linear in log scale is exponential. |
Fairplay medal of dnaleor's trading simulator. 
|
|
|
|
Raystonn (OP)
|
 |
June 18, 2014, 05:18:28 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
It's an illusion. S curve has no vertical stage, just like an exponential curve doesn't have it. The rate of adoption is already (and had always been) exponential, that's why it looks like straight line on the log-scale chart. No. The rate of adoption is currently linear. The Metcalfe value is exponential. That is the number of unique addresses used per day, squared. Vertical is an expression. The middle of an S curve looks nearly vertical. Look at left side of the OP chart: it is in log scale. Curve that looks linear in log scale is exponential. I *am* the OP. The Metcalfe value displayed on the chart is the rate of adoption, *squared*. That is the definition of the value from Metcalfe's Law. |
|
|
|
|
rogerwilco
Member
 
 Offline Offline
Activity: 107
Merit: 10

|
 |
June 18, 2014, 05:24:10 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
It's an illusion. S curve has no vertical stage, just like an exponential curve doesn't have it. The rate of adoption is already (and had always been) exponential, that's why it looks like straight line on the log-scale chart. Actually, the S-curve is the colloquial term for the Logistic function, which can be intuitively understood as a system initially taking on exponential growth but eventually running into limiting factors. The fastest rate of expansion ("going vertical") is halfway between the lower and upper limits. This inflection point represents a paradigm shift, because whereas before the growth could seemingly expand anywhere in the system, now it's become the norm so there are fewer places left to expand into. As an example, in the outside chance Bitcoin becomes the world reserve currency, this would be the point at which people would no longer value a bitcoin in dollars, but rather value a dollar in terms of bitcoins. |
|
|
|
|
|
Wary
|
 |
June 18, 2014, 05:36:34 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
It's an illusion. S curve has no vertical stage, just like an exponential curve doesn't have it. The rate of adoption is already (and had always been) exponential, that's why it looks like straight line on the log-scale chart. No. The rate of adoption is currently linear. The Metcalfe value is exponential. That is the number of unique addresses used per day, squared. Vertical is an expression. The middle of an S curve looks nearly vertical. Look at left side of the OP chart: it is in log scale. Curve that looks linear in log scale is exponential. I *am* the OP. The Metcalfe value displayed on the chart is the rate of adoption, *squared*. That is the definition of the value from Metcalfe's Law. That's why I'm surprised. On the chart we can see a curve that fluctuates around a straight line. Correct? The vertical scale is log. Correct? Therefore the straight line is an exponential line. Because no other line can be straight in the log scale. Correct? Therefore rate of adoption (squared) fluctuates around an exponential rate. Correct? Exponential line squared is still an exponential line. Correct? Therefore rate of adoption grows at an exponential rate. Correct? Now the S-curve. It is basically an exponential curve that at it's last third slows down to horizontal line. Until that stage it's rate of growth is constant. Say, it grows 10x each year. It was growing this way at the beginning, it grows that way now, it will keep growing this way till it starts slowing down. The rate of growth in relative number, percentage-wise will never increase. That's why I said that S-curve has no vertical stage. The area that you are referring to as "vertical stage" is the area somewhere around 50% where the growth in absolute numbers, will reach the maximum. But the growth rate in relative numbers, in %, will be decreasing by then and will be lower than it is now. Edit: typo |
Fairplay medal of dnaleor's trading simulator. 
|
|
|
kashish948
Legendary

 Offline Offline
Activity: 1582
Merit: 1000

|
 |
June 18, 2014, 05:41:48 AM |
|
the price will keep increasing with new merchants especially the big ones!
|
|
|
|
|
|
Wary
|
 |
June 18, 2014, 05:57:59 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price. Sorry, one more correction: Super-exponential curve is a curve that looks exponential on log scale. Something like y=exp(exp(x)). While exponential curve, squared, is still just an exponential: y = (exp(x))^2 = exp(2x). In log scale it will still looks like straight line, just more steep, than non-squared one. P.S. Sorry for nitpicking, nothing personal (and thanks for the OP), I just wanted to clarify some math details. |
Fairplay medal of dnaleor's trading simulator. 
|
|
|
|
Raystonn (OP)
|
 |
June 18, 2014, 06:21:28 AM |
|
That's why I'm surprised. On the chart we can see a curve that fluctuates around a straight line. Correct? The vertical scale is log. Correct? Therefore the straight line is an exponential line. Because no other line can be straight in the log scale. Correct? Therefore rate of adoption (squared) fluctuates around an exponential rate. Correct? Exponential line squared is still an exponential line. Correct? Therefore rate of adoption grows at an exponential rate. Correct?
Right now adoption is increasing at a linear rate. This means we gain more users at some average constant rate of new addresses per day. The Metcalfe value is this value squared. So, to approximate, N(y) = y^2, where N is the number of addresses and y the year number. N increases exponentially as time marches on in a linear fashion. As we approach the center of the S curve, adoption will begin increasing at an exponential rate. The Metcalfe value is this exponential rate, squared. So, to approximate, N(y) = (y^2)^2, where N is the number of addresses and y the year number. This is simplified to N(y) = y^4. N increases much faster here. Now the S-curve. It is basically an exponential curve that at it's last third slows down to horizontal line. Until that stage it's rate of growth is constant.
I will stop you here. What you describe is not an S curve. This is an S curve:  |
|
|
|
|
Swordsoffreedom
Legendary

 Offline Offline
Activity: 3346
Merit: 1196
Leading Crypto Sports Betting & Casino Platform


|
 |
June 18, 2014, 06:22:38 AM |
|
Thanks for the chart I was wondering what the chart looks like normalized for Price Volatility
I assume that as the market price moves upward or downward that the price affects the users and unique transactions that occur in the network
That said more data is always a good thing
|
| ..Stake.com.. | | | ▄████████████████████████████████████▄
██ ▄▄▄▄▄▄▄▄▄▄ ▄▄▄▄▄▄▄▄▄▄ ██ ▄████▄
██ ▀▀▀▀▀▀▀▀▀▀ ██████████ ▀▀▀▀▀▀▀▀▀▀ ██ ██████
██ ██████████ ██ ██ ██████████ ██ ▀██▀
██ ██ ██ ██████ ██ ██ ██ ██ ██
██ ██████ ██ █████ ███ ██████ ██ ████▄ ██
██ █████ ███ ████ ████ █████ ███ ████████
██ ████ ████ ██████████ ████ ████ ████▀
██ ██████████ ▄▄▄▄▄▄▄▄▄▄ ██████████ ██
██ ▀▀▀▀▀▀▀▀▀▀ ██
▀█████████▀ ▄████████████▄ ▀█████████▀
▄▄▄▄▄▄▄▄▄▄▄▄███ ██ ██ ███▄▄▄▄▄▄▄▄▄▄▄▄
██████████████████████████████████████████ | | | | | | ▄▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▄
█ ▄▀▄ █▀▀█▀▄▄
█ █▀█ █ ▐ ▐▌
█ ▄██▄ █ ▌ █
█ ▄██████▄ █ ▌ ▐▌
█ ██████████ █ ▐ █
█ ▐██████████▌ █ ▐ ▐▌
█ ▀▀██████▀▀ █ ▌ █
█ ▄▄▄██▄▄▄ █ ▌▐▌
█ █▐ █
█ █▐▐▌
█ █▐█
▀▄▄▄▄▄▄▄▄▄▄▄▄▄▄▄▄▄▄▀█ | | | | | | ▄▄█████████▄▄
▄██▀▀▀▀█████▀▀▀▀██▄
▄█▀ ▐█▌ ▀█▄
██ ▐█▌ ██
████▄ ▄█████▄ ▄████
████████▄███████████▄████████
███▀ █████████████ ▀███
██ ███████████ ██
▀█▄ █████████ ▄█▀
▀█▄ ▄██▀▀▀▀▀▀▀██▄ ▄▄▄█▀
▀███████ ███████▀
▀█████▄ ▄█████▀
▀▀▀███▄▄▄███▀▀▀ | | | ..PLAY NOW.. |
|
|
|
|
Wary
|
 |
June 18, 2014, 07:08:56 AM |
|
N(y) = y^2, where N is the number of addresses and y the year number. N increases exponentially as time marches on in a linear fashion. As we approach the center of the S curve, adoption will begin increasing at an exponential rate. The Metcalfe value is this exponential rate, squared. So, to approximate, N(y) = (y^2)^2, where N is the number of addresses and y the year number. This is simplified to N(y) = y^4. N increases much faster here. OK. I think I get the root of our misunderstanding. You seem to think that y^2 or y^4 is an exponent. It is not. If you don't trust me, ask somebody whom you trust.  I will stop you here. What you describe is not an S curve. This is an S curve: rogerwilco already posted reference to the the S-curve aka logistic function: http://en.wikipedia.org/wiki/Logistic_function. In particular, this article says: " the logistic curve shows early exponential growth for negative argument, which slows to linear growth of slope 1/4 for an argument near zero, then approaches one with an exponentially decaying gap.". Which means exactly what I've said: exponential curve that slows down to horizontal line. Again, sorry for bothering you with calculus 101. |
Fairplay medal of dnaleor's trading simulator. 
|
|
|
zimmah
Legendary

 Offline Offline
Activity: 1106
Merit: 1005

|
 |
June 18, 2014, 07:10:02 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
Funny how human psychology makes most humans buy when the price is rising , but no one dares buying when the price is low after a bubble. Even when it's pretty obvious a new bubble will come. I mean right now we are sitting on 600s but people will only really start buying once we past 1000 or so. And then once we peaked at about 5000 or so, people will stop buying until we are once again past the previous ATH rather than just buying during the downtrend. |
|
|
|
|
|
Raystonn (OP)
|
 |
June 18, 2014, 07:46:47 AM |
|
I've been analyzing further. When we hit the vertical stage of the adoption S curve, rate of adoption will go exponential. Metcalfe will go super-exponential at that point, along with price.
Funny how human psychology makes most humans buy when the price is rising , but no one dares buying when the price is low after a bubble. Even when it's pretty obvious a new bubble will come. I mean right now we are sitting on 600s but people will only really start buying once we past 1000 or so. And then once we peaked at about 5000 or so, people will stop buying until we are once again past the previous ATH rather than just buying during the downtrend. Without buyers near the top, we'd have no one to sell to. I plan to keep no more than 90% of my liquid wealth in Bitcoin. I will need to sell at regular price intervals to keep that ratio. |
|
|
|
|
|
Raystonn (OP)
|
 |
June 18, 2014, 07:49:03 AM |
|
N(y) = y^2, where N is the number of addresses and y the year number. N increases exponentially as time marches on in a linear fashion. As we approach the center of the S curve, adoption will begin increasing at an exponential rate. The Metcalfe value is this exponential rate, squared. So, to approximate, N(y) = (y^2)^2, where N is the number of addresses and y the year number. This is simplified to N(y) = y^4. N increases much faster here. OK. I think I get the root of our misunderstanding. You seem to think that y^2 or y^4 is an exponent. It is not. If you don't trust me, ask somebody whom you trust.  I will stop you here. What you describe is not an S curve. This is an S curve: rogerwilco already posted reference to the the S-curve aka logistic function: http://en.wikipedia.org/wiki/Logistic_function. In particular, this article says: " the logistic curve shows early exponential growth for negative argument, which slows to linear growth of slope 1/4 for an argument near zero, then approaches one with an exponentially decaying gap.". Which means exactly what I've said: exponential curve that slows down to horizontal line. Again, sorry for bothering you with calculus 101. I think you are just playing at definitions and missing the larger point. As rate of adoption increases beyond linear, rate of price appreciation will increase beyond the current exponential. Until we pass the 50% point on the S curve, the rate of price appreciation should therefore accelerate, not diminish. |
|
|
|
|
|



