|
MrFreeDragon
|
 |
August 31, 2019, 12:56:56 PM |
|
multicore in process, wait..
to be continue..
Thak you! Nice job :-) By the way, can you explain why do you need 10 Ntimeit? It actually finds the key from the 1st time, and the 2nd, 3d, etc finds the same key (for #32 as i tested). So, what is the reason for doing the same 10 times? And also, can you confirm that in this Kangaroo method the luck also is important (for high order pubkeys)? |
|
|
|
|
|
|
The Bitcoin network protocol was designed to be extremely flexible. It can be used to create timed transactions, escrow transactions, multi-signature transactions, etc. The current features of the client only hint at what will be possible in the future.
|
|
|
Advertised sites are not endorsed by the Bitcoin Forum. They may be unsafe, untrustworthy, or illegal in your jurisdiction.
|
|
|
racminer
Member
 
 Offline Offline
Activity: 242
Merit: 17

|
 |
August 31, 2019, 11:33:33 PM |
|
.......................
multicore in process, wait..
to be continue..
Maybe you can split equally the search range among threads ... |
|
|
|
|
bulleteyedk
Jr. Member

 Offline Offline
Activity: 84
Merit: 1

|
 |
September 01, 2019, 03:04:56 PM |
|
I read again most of the results posted here, and collected them to one table. Of corse results could differ from card to card depending on the settings. I also add the price of the CUDA. I tried to collect some benchmark. If you have some other device - pls, do not hesitate to add  1. RTX 2080ti 1,200-1,300M key/sec (price $1,200-1,500)
2. GTX 1070 250 Mkey/sec (price $450-550)
3. GTX 1080ti 150 Mkey/sec (price $700-1,000)
4. GTX 680 109 Mkey/sec (price $150)
5. RX 480 107 Mkey/sec (price $130-150)
6. RX 470 105 Mkey/sec (price $150-300)
7. RX 580 89 Mkey/sec (price $200-250)
8. RX 560 50 Mkey/sec (price $100-150)
9. R9 280/290x 20 Mkey/sec (price $50)
Thanks for making this table, i've just tested one of my kids' GTX 770 2GB card and its capable of doing 120MKey/sec |
|
|
|
|
|
MrFreeDragon
|
 |
September 01, 2019, 06:09:39 PM Merited by vapourminer (1) |
|
Table update with bitcrack key/rate per sec: 1. RTX 2080ti 1,200-1,300 Mkey/sec (price $1,200-1,500)
2. GTX 2070ti 805 MMkey/sec
2. GTX 1080ti 345 Mkey/sec (price $700-1,000)
3. GTX 1080 130 Mkey/sec (price $500)
3. GTX 1070ti 100 Mkey/sec
3. GTX 1070 80-90 Mkey/sec (price $450-550)
3. GTX 1060 69 Mkey/sec
4. GTX 1050ti 64 Mkey/sec (price $150-200)
4. GTX 980 70-80 Mkey/sec
4. GTX 770(2Gb) 120 MKey/sec
4. GTX 680 109 Mkey/sec (price $150)
4. GT 640 9 Mkey/sec
5. RX 480 107 Mkey/sec (price $130-150)
6. RX 470 105 Mkey/sec (price $150-300)
7. RX 580 89 Mkey/sec (price $200-250)
8. RX 560 50 Mkey/sec (price $100-150)
9. R9 280/290x 20 Mkey/sec (price $50)
|
|
|
|
|
MrFreeDragon
|
 |
September 01, 2019, 06:19:36 PM |
|
Thanks for making this table, i've just tested one of my kids' GTX 770 2GB card and its capable of doing 120MKey/sec
How could you manage this? Are you really sure in 120 Mkey/sec with GTX 770? This card GTX 770 cost not so much, and in comparison with GTX 1080ti you can need 3 cards GTX 770 and for the the same (or more) Key/sec rate. But the cost will be 2 times less. |
|
|
|
|
zielar (OP)
|
 |
September 01, 2019, 06:31:29 PM |
|
Thanks for making this table, i've just tested one of my kids' GTX 770 2GB card and its capable of doing 120MKey/sec
How could you manage this? Are you really sure in 120 Mkey/sec with GTX 770? This card GTX 770 cost not so much, and in comparison with GTX 1080ti you can need 3 cards GTX 770 and for the the same (or more) Key/sec rate. But the cost will be 2 times less. GTX 770 = price ~$80-90 GTX 980 = price ~$150-160 GTX 1060 = price ~$240-260 GTX 1070Ti = price ~$280-300 GT 640 = price ~$10-15 Tesla V100 16GB - 1570-1600 Mkey/s = price ~$10000 |
If you want - you can send me a donation to my BTC wallet address 31hgbukdkehcuxcedchkdbsrygegyefbvd
|
|
|
Telariust
Jr. Member

 Offline Offline
Activity: 38
Merit: 18

|
 |
September 01, 2019, 06:38:49 PM |
|
compare >cuBitCrack -c -d 0 1AVJKwzs9AskraJLGHAZPiaZcrpDr1U6AB
[2019-09-01.21:24:56] [Info] Compression: compressed
...
[2019-09-01.21:24:56] [Info] Initializing GeForce GTX 1070
[2019-09-01.21:24:56] [Info] Generating 262,144 starting points (10.0MB)
...
GeForce GTX 1070 232/8192MB | 1 target 73.28 MKey/s (403,701,760 total) [00:00:10]
and >cuBitCrack -c -d 0 -b 15 -t 512 -p 1024 1AVJKwzs9AskraJLGHAZPiaZcrpDr1U6AB
[2019-09-01.21:24:56] [Info] Compression: compressed
...
[2019-09-01.21:23:20] [Info] Initializing GeForce GTX 1070
[2019-09-01.21:23:21] [Info] Generating 7,864,320 starting points (300.0MB)
...
GeForce GTX 1070 928/8192MB | 1 target 241.32 MKey/s (1,753,743,360 total) [00:00:10]
see? need new column - optimal argv i know # GTX1060 = -b 9 -t 512 -p 1024 # GTX1070 = -b 15 -t 512 -p 1024 # GTX1080Ti= -b 28 -t 512 -p 1024 and 2cols of hashrate - with default and with optimal argv ..and its good content for add to 1post |
|
|
|
|
bulleteyedk
Jr. Member

 Offline Offline
Activity: 84
Merit: 1

|
 |
September 01, 2019, 08:15:23 PM
Last edit: September 01, 2019, 08:59:32 PM by bulleteyedk Merited by vapourminer (1) |
|
Thanks for making this table, i've just tested one of my kids' GTX 770 2GB card and its capable of doing 120MKey/sec
How could you manage this? Are you really sure in 120 Mkey/sec with GTX 770? This card GTX 770 cost not so much, and in comparison with GTX 1080ti you can need 3 cards GTX 770 and for the the same (or more) Key/sec rate. But the cost will be 2 times less. I was expecting that GTX 770 to be in that area, as i have a GTX 680 running in my own PC, that scores 109-110 MKey/sec. The parameters i use for my own setup was slightly altered, but mainly they are the same as for my own setup. 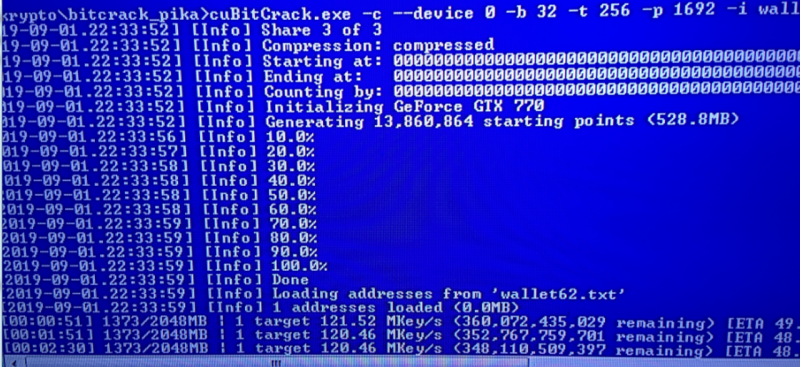 Actually i think especially in regards to the cuda version of bitcrack, the number of cuda cores for the specific card is really important, and there is actually a bunch of older cards with some great numbers here, for ex. the GTX 680 have 1536 cuda cores, which also happends to be the number of cuda cores for the GTX 770. For comparison other cards cuda cores: RTX 2080 TI - 4352 GTX 1080 TI - 3583 RTX 2080 Super - 3072 RTX 2080 Gaming - 2944 GTX 780 TI - 2880 GTX 980 TI - 2816 GTX 2070 TI - 2560 GTX 1080 - 2560 RTX 2070 Gaming - 2304 GTX 780 - 2304 RTX 2060 Super - 2176 GTX 980 - 2048 RTX 2060 - 1920 GTX 1070 - 1920 GTX 1060 1708 GTX 1660 TI - 1536 GTX 770 - 1536 GTX 680 - 1536 GTX 1660 Dual OC - 1408 GTX 670 - 1344 GTX 1660 Armor - 1280 GTX 1060 - 1152 GTX 760 - 1152 GTX 1650 - 896 GTX 1050 TI - 768 GTX 1050 - 640 GTX 580 - 512 Due to this challenge i have actually been on the lookout for a cheap and used GTX 780 TI - but not succeeded in finding anyone in my price target yet, im exitied to see how much this card can deliver  |
|
|
|
|
|
MrFreeDragon
|
 |
September 02, 2019, 12:16:46 AM |
|
Here is nice comparison of the most popular models: Product Name Cores TMUs ROPs
GeForce RTX 2080 Ti 4352 272 88
Radeon RX 5700 XT 2560 160 64
Radeon Vega 8 512 32 8
Radeon RX 580 2304 144 32
Radeon RX 570 2048 128 32
GeForce RTX 2060 1920 120 48
GeForce RTX 2070 SUPER 2560 160 64
GeForce RTX 2070 2304 144 64
GeForce GTX 1660 Ti 1536 96 48
GeForce GTX 1050 Ti 768 48 32
GeForce GTX 1080 Ti 3584 224 88
GeForce GTX 1650 896 56 32
GeForce RTX 2080 2944 184 64
GeForce GTX 750 Ti 640 40 16
GeForce GTX 1060 6 GB 1280 80 48
Radeon RX 5700 2304 144 64
GeForce GTX 1660 1408 88 48
GeForce GTX 1080 2560 160 64
GeForce RTX 2060 SUPER 2176 136 64
GeForce GTX 1070 1920 120 64
GeForce GTX 970 1664 104 56
Radeon RX Vega 11 704 44 8
GeForce RTX 2080 SUPER 3072 192 64
HD Graphics 4000 128 16 2
GeForce 210 16 8 4
Radeon R5 Graphics 128 8 4
GeForce GTX 960 1024 64 32
Radeon RX Vega 56 3584 224 64
Radeon VII 3840 240 64
GeForce GTX 1050 640 40 32
Radeon RX 590 2304 144 32
Radeon RX 480 2304 144 32
Radeon HD 5450 80 8 4
Radeon RX 470 2048 128 32
GeForce GTX 980 Ti 2816 176 96
Radeon RX Vega 64 4096 256 64
Radeon RX 560 1024 64 16
GeForce GT 1030 384 24 16
HD Graphics 4600 160 20 2
GeForce GTX 1070 Ti 2432 152 64
Quadro 4000 256 32 32
Radeon RX 550 512 32 16
Radeon R9 280X 2048 128 32
Xbox One X GPU 2560 160 32
Radeon R4 Graphics 128 8 4
Radeon HD 6450 160 8 4
Radeon HD 5770 800 40 16
GeForce GTX 980 2048 128 64
GeForce GTX 1650 Ti 1024 64 32
GeForce GTX 660 960 80 24
|
|
|
|
brainless
Member
 
 Offline Offline
Activity: 318
Merit: 34

|
 |
September 02, 2019, 06:03:59 PM |
|
#!/usr/bin/python
# by 57fe (fe57.org/forum/thread.php?board=4&thema=1#1)
#######################
# print() compatibility python 2/3
from __future__ import print_function
#######################
# settings
pow2pubkey = 32 # bits/order/pow2/exp key
pow2kangaroo = 3 # discriminator
Ntimeit = 10 # times for avg runtime
prngseed = 0 # 0,any
flag_debug = 0 # 0,1,2,3
#######################
# low order pubkeys
pubkeys = {
16: ('029d8c5d35231d75eb87fd2c5f05f65281ed9573dc41853288c62ee94eb2590b7a', 0xc936)
, 24: ('036ea839d22847ee1dce3bfc5b11f6cf785b0682db58c35b63d1342eb221c3490c', 0xdc2a04)
, 32: ('0209c58240e50e3ba3f833c82655e8725c037a2294e14cf5d73a5df8d56159de69', 0xb862a62e)
, 33: ('02ed949eaca31df5e8be9bf46adc1dfae1734b8900dcc303606831372955c728da', False) #0x01abcd1234
, 40: ('03a2efa402fd5268400c77c20e574ba86409ededee7c4020e4b9f0edbee53de0d4', 0xe9ae4933d6)
, 45: ('026ecabd2d22fdb737be21975ce9a694e108eb94f3649c586cc7461c8abf5da71a', 0x122fca143c05)
, 50: ('03f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6', 0x022bd43c2e9354)
, 65: ('0230210c23b1a047bc9bdbb13448e67deddc108946de6de639bcc75d47c0216b1b', 0x01a838b13505b26867)
,105: ('03bcf7ce887ffca5e62c9cabbdb7ffa71dc183c52c04ff4ee5ee82e0c55c39d77b', False)
}
#######################
# import
import os
import sys
import time
import random
try:
# https://www.lfd.uci.edu/~gohlke/pythonlibs/
import gmpy2
except:
flag_gmpy2 = False
print("[warn] gmpy2 not found. raw python is slow!")
else:
flag_gmpy2 = True
try:
from coincurve import PrivateKey, PublicKey
from coincurve.utils import int_to_bytes, hex_to_bytes, bytes_to_int, bytes_to_hex, int_to_bytes_padded
except:
flag_coincurve = False
#print("[warn] coincurve not found. random pubkey not available!")
else:
flag_coincurve = True
if 0:
from multiprocessing import Pool
from multiprocessing import cpu_count
from multiprocessing import freeze_support
#######################
# python 2,3
#import sys
#import time
if sys.version_info[0] == 2:
from time import clock
else:
from time import perf_counter
from time import process_time
clock = time.perf_counter
xrange=range
raw_input=input
#######################
# secp256k1
#modulo = 2**256-2**32-2**9-2**8-2**7-2**6-2**4-1
modulo = 115792089237316195423570985008687907853269984665640564039457584007908834671663
order = 115792089237316195423570985008687907852837564279074904382605163141518161494337
#modulo = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
#order = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
Gx = 55066263022277343669578718895168534326250603453777594175500187360389116729240
Gy = 32670510020758816978083085130507043184471273380659243275938904335757337482424
#Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
#Gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
class Point:
def __init__(self, x=0, y=0):
self.x = x
self.y = y
Gp = Point(Gx,Gy)
Zp = Point(0,0) # zero-point, infinite in real x,y - plane
#######################
# functions
# return (g, x, y) a*x + b*y = gcd(x, y)
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, x, y = egcd(b % a, a)
return (g, y - (b // a) * x, x)
def rev(b, n=modulo):
while b < 0:
b += n
g, x, _ = egcd(b, n)
if g == 1:
return x % n
def mul2(P, p=modulo):
R = Point()
if flag_gmpy2:
c = 3 * P.x * P.x * gmpy2.invert(2*P.y, p) % p
else:
c = 3 * P.x * P.x * rev(2*P.y, p) % p
R.x = (c*c - 2*P.x) % p
R.y = (c*(P.x - R.x) - P.y) % p
return R
# 1I, 3M
def add(P, Q, p=modulo):
R = Point()
dx = Q.x - P.x
dy = Q.y - P.y
if flag_gmpy2: # 1I, 1M
c = dy * gmpy2.invert(dx, p) % p
else:
c = dy * rev(dx, p) % p
R.x = (c*c - P.x - Q.x) % p # 1M
R.y = (c*(P.x - R.x) - P.y) % p # 1M
return R
def mulk(k, P=Gp, p=modulo):
if k == 0: return Zp
elif k == 1: return P
elif (k % 2 == 0):
return mulk(k/2, mul2(P, p), p)
else:
return add(P, mulk( (k-1)/2, mul2(P, p), p), p)
def newX2Y(X, y_parity):
p = modulo
Y = 3
tmp = 1
while Y:
if Y & 1:
tmp = tmp*X % p
Y >>= 1
X = X*X % p
X = (tmp+7) % p
Y = (p+1)//4
tmp = 1
while Y:
if Y & 1:
tmp = tmp*X % p
Y >>= 1
X = X*X % p
Y = tmp
if Y%2 != y_parity:
Y = -Y % p
return Y
def KANGAROO():
DP_rarity = 1 << ((pow2pubkey - 2*pow2kangaroo)//2 - 2)
if flag_debug > 0:
print("[DP_rarity] 1<<((pow2pub - 2*pow2k) -2) = 1<<((%s-2*%s)//2 -2) = %s" % (pow2pubkey,pow2kangaroo,DP_rarity))
jump_modulo = ((pow2pubkey-1) // 2) + pow2kangaroo
if flag_debug > 0:
print("[jump_modulo] (pow2pub-1)//2 + pow2k = (%s-1)//2 + %s = %s" % (pow2pubkey,pow2kangaroo,jump_modulo))
T, t, dt = [], [], []
W, w, dw = [], [], []
if flag_debug > 0:
print( '[t] 3<<(pow2pub-2) + rng(1,(1<<(pow2pub-1))) = 3<<(%s-2) + rng(1,(1<<(%s-1))) = %s + %s' %
( pow2pubkey, pow2pubkey
,3<<(pow2pubkey-2), random.randint(1, (1<<(pow2pubkey-1)))
)
)
for k in range(Nt):
t.append((3 << (pow2pubkey - 2)) + random.randint(1, (1 << (pow2pubkey - 1))))#-(1 << (pow2pubkey - 2)) )
T.append(mulk(t[k]))
dt.append(0)
for k in range(Nw):
w.append(random.randint(1, (1 << (pow2pubkey - 1))))
W.append(add(W0,mulk(w[k])))
dw.append(0)
print('[+] T+W ready')
n_jump = last_jump = 0
prvkey = False;
A, Ak, B, Bk = [], [], [], []
t0 = t1 = t2 = time.time()
while (1):
if flag_debug > 2: print('[new_loop] %s jumps'%n_jump)
for k in range(Nt):
if flag_debug > 2: print('[k/Nt] %s/%s'%(k+1,Nt))
n_jump += 1
pw = T[k].x % jump_modulo
pw = int(pw)
dt[k] = 1 << pw
if T[k].x % (DP_rarity) == 0:
A.append(T[k].x)
Ak.append(t[k])
if flag_debug > 1:
print('[tame] A=%s, B=%s'%(len(A),len(B)))
if flag_debug > 0:
save2file('tame.txt', 'a', '%064x %s\n'%(T[k].x,t[k]) )
result = list(set(A) & set(B))
if len(result) > 0:
sol_kt = A.index(result[0])
sol_kw = B.index(result[0])
prvkey = Ak[sol_kt] - Bk[sol_kw]
if prvkey: break
t[k] += dt[k]
T[k] = add(P[pw], T[k])
if prvkey: break
for k in range(Nw):
if flag_debug > 2: print('[k/Nw] %s/%s'%(k+1,Nw))
n_jump += 1
pw = W[k].x % jump_modulo
pw = int(pw)
dw[k] = 1 << pw
if W[k].x % (DP_rarity) == 0:
B.append(W[k].x)
Bk.append(w[k])
if flag_debug > 1:
print('[wild] A=%s, B=%s'%(len(A),len(B)))
if flag_debug > 0:
save2file('wild.txt', 'a', '%064x %s\n'%(W[k].x,w[k]) )
result = list(set(A) & set(B))
if len(result) > 0:
sol_kt = A.index(result[0])
sol_kw = B.index(result[0])
prvkey = Ak[sol_kt] - Bk[sol_kw]
if prvkey: break
w[k] += dw[k]
W[k] = add(P[pw], W[k])
if prvkey: break
t2 = time.time()
if (t2-t1) > 1:
if sys.version_info[0] == 2:
print('\r[~] %.1f j/s'%((n_jump-last_jump)/(t2-t1)), end='')
sys.stdout.flush()
else:
print('\r[~] %.1f j/s'%((n_jump-last_jump)/(t2-t1)), end='', flush=True )
t1 = t2
last_jump = n_jump
return prvkey, n_jump, (time.time()-t0)
def save2file(path, mode, data):
fp = open(path, mode)
if type(data) in (list,tuple,dict):
fp.writelines(data)
else:
#elif type(data) in (str,int):
fp.write(data)
fp.close()
def usage():
print('[usage] %s [bits] [pubkey]'%(sys.argv[0]))
print(' %s 32'%(sys.argv[0]))
print(' %s 32 %s'%(sys.argv[0],pubkeys[32][0]))
exit(-1)
#######################
#main
if __name__ == '__main__':
#print('[os] %s' % os.name)
if os.name == 'nt':
#freeze_support()
pass
print("[################################################]")
print("[# ECDSA Pollard-kangaroo PrivKey Recovery Tool #]")
print("[# based on code by 57fe 2019 #]")
print("[# singlecore #]");
#print("[# multicore #]");
print("[################################################]")
if len(sys.argv) > 1 and str(sys.argv[1]) in ('--help','-h','/?') :
usage()
print('[date] {}'.format(time.ctime()))
print("[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]")
if prngseed in (0,'0',False,'False','false',''):
prngseed = random.randint(1,2**32)
random.seed(prngseed)
print('[PRNGseed] %s' % prngseed)
if len(sys.argv) > 1 :
try:
pow2pubkey=int(sys.argv[1])
except:
usage()
if pow2pubkey < 1 or pow2pubkey > 256 :
print("[error] bits must be in range 1..256!")
usage()
print('[bits] 2^%s %s' % (pow2pubkey, '(warn: too big!)' if pow2pubkey>50 else ''))
if len(sys.argv) > 2 :
prvkey0 = False
pubkey0 = str(sys.argv[2])
print('[i] pubkey#%s loaded from argv2' % pow2pubkey)
elif flag_coincurve:
prvkey0 = random.randint(1,2**pow2pubkey)
pubkey0 = bytes_to_hex(PublicKey.from_secret(int_to_bytes_padded(prvkey0)).format(1))
#pubkey0 = bytes_to_hex(PublicKey.from_secret(int_to_bytes_padded(prvkey0)).format(0))
print('[i] pubkey#%s randomly generated' % pow2pubkey)
else:
pubkey0, prvkey0 = pubkeys[pow2pubkey]
print('[i] pubkey#%s loaded from default table' % pow2pubkey)
else:
print('[bits] 2^%s %s' % (pow2pubkey, '(warn: too big!)' if pow2pubkey>50 else ''))
pubkey0, prvkey0 = pubkeys[pow2pubkey]
print('[i] pubkey#%s loaded from default table' % pow2pubkey)
if prvkey0 not in (0,'0',False,'False','false',''):
print('[prvkey#%s] 0x%064x' % (pow2pubkey,prvkey0))
print('[pubkey#%s] %s' % (pow2pubkey,pubkey0))
#calc Y if pubkey is compress
if len(pubkey0)==130:
X = int(pubkey0[2:66], 16)
Y = int(pubkey0[66:],16)
print("[format] uncompressed")
elif len(pubkey0)==66:
X = int(pubkey0[2:66], 16)
Y = newX2Y(X,int(pubkey0[:2])-2)
print("[format] compressed")
else:
print("[error] pubkey len(66/130) invalid!")
usage()
print("[Xcoordinate] %064x" % X)
print("[Ycoordinate] %064x" % Y)
W0 = Point(X,Y)
print("[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]")
starttime = time.time()
P = [Gp]
for k in range(255): P.append(mul2(P[k]))
print('[+] P-table ready')
Nt = Nw = 2**pow2kangaroo
if flag_debug > 0:
print("[range(L..U)] 1..2^%s(0x%x)" % (pow2pubkey, 2**pow2pubkey))
print("[w=U-L] 0x%x ; w/2=0x%x" % (2**pow2pubkey, 2**(pow2pubkey-1)))
print("[pow2k] 2^%s: Nt=%s, Nw=%s" % (pow2kangaroo,Nt,Nw))
jumps_list = []
runtime_list = []
#timeit
for i in range(Ntimeit):
print("[~~~~~~~~~~~~~~~~~~~~~~~[%s]~~~~~~~~~~~~~~~~~~~~~~]"%(i+1))
if flag_debug > 0:
save2file('tame.txt', 'w', '')
save2file('wild.txt', 'w', '')
prvkey, n_jump, runtime = KANGAROO()
jumps_list.append(n_jump)
runtime_list.append(runtime)
print('')
print('[prvkeyX] %064x' % (prvkey) )
save2file('results.txt', 'a', ('%064x\n'%prvkey, '---------------\n'))
if prvkey0 not in (0,'0',False,'False','false',''):
print('[prvkey0] %064x' % (prvkey0))
if prvkey == prvkey0:
print('[double-check] success!')
else:
print('[double-check] failed!')
print('[jump] %s' % n_jump)
print('[time] %.1f sec' % runtime)
print("[################################################]")
if Ntimeit > 1:
M = sum(jumps_list)*1.0 / len(jumps_list)
print('[(avg)jump] %.0f' % (M) )
#D = sum((xi - M) ** 2 for xi in jumps_list)*1.0 / len(jumps_list)
#print('[(avg)jum2] %.1f +/- %.1f' % (M, (D/(len(jumps_list)-1))**0.5) )
print('[(avg)time] %.1f sec' % (sum(runtime for runtime in runtime_list)/Ntimeit) )
#print('[(avg)tim2] %.1f sec' % ((time.time()-starttime)/Ntimeit) )
else:
pass
print("[################################################]")
print('[date] {}'.format(time.ctime()))
#print('[exit] exit')
#print('');raw_input('Press ENTER to continue...');print('')
exit(0)
Addon needed remove pubkeys = xxxxxx add example ** with open("pubkeys.txt", "r") as m: add = m.read().split() for ad in add: *** multi pubkeys at once check inside bit range this script check only 1 pubkey in bit range |
13sXkWqtivcMtNGQpskD78iqsgVy9hcHLF
|
|
|
PrivatePerson
Member
 
 Offline Offline
Activity: 173
Merit: 12

|
 |
September 03, 2019, 02:04:37 PM
Last edit: September 03, 2019, 02:14:43 PM by PrivatePerson |
|
Kangaroo System, test friends.
Can you share your scan time and speed?
and How many bits?
I'm
48 bit - 110k / s - 87 sec
51 bit - 110k / s - 200 sec
[################################################]
[# ECDSA Pollard-kangaroo PrivKey Recovery Tool #]
[# based on code by 57fe 2019 #]
[# singlecore #]
[################################################]
[date] Tue Sep 3 17:52:34 2019
[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]
[PRNGseed] 439144377
[bits] 2^50
[i] pubkey#50 loaded from default table
[prvkey#50] 0x00000000000000000000000000000000000000000000000000022bd43c2e9354
[pubkey#50] 03f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6
[format] compressed
[Xcoordinate] f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6
[Ycoordinate] eb3dfcc04c320b55c529291478550be6072977c0c86603fb2e4f5283631064fb
[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]
[+] P-table ready
[~~~~~~~~~~~~~~~~~~~~~~~[1]~~~~~~~~~~~~~~~~~~~~~~]
[+] T+W ready
[~] 144975.9 j/s
[prvkeyX] 00000000000000000000000000000000000000000000000000022bd43c2e9354
[prvkey0] 00000000000000000000000000000000000000000000000000022bd43c2e9354
[double-check] success!
[jump] 82359278
[time] 570.5 sec what does 3 column mean? And why do 33 and 105 matter False? pubkeys = {
16: ('029d8c5d35231d75eb87fd2c5f05f65281ed9573dc41853288c62ee94eb2590b7a', 0xc936)
, 24: ('036ea839d22847ee1dce3bfc5b11f6cf785b0682db58c35b63d1342eb221c3490c', 0xdc2a04)
, 32: ('0209c58240e50e3ba3f833c82655e8725c037a2294e14cf5d73a5df8d56159de69', 0xb862a62e)
, 33: ('02ed949eaca31df5e8be9bf46adc1dfae1734b8900dcc303606831372955c728da', False) #0x01abcd1234
, 40: ('03a2efa402fd5268400c77c20e574ba86409ededee7c4020e4b9f0edbee53de0d4', 0xe9ae4933d6)
, 45: ('026ecabd2d22fdb737be21975ce9a694e108eb94f3649c586cc7461c8abf5da71a', 0x122fca143c05)
, 50: ('03f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6', 0x022bd43c2e9354)
, 65: ('0230210c23b1a047bc9bdbb13448e67deddc108946de6de639bcc75d47c0216b1b', 0x01a838b13505b26867)
,105: ('03bcf7ce887ffca5e62c9cabbdb7ffa71dc183c52c04ff4ee5ee82e0c55c39d77b', False) |
|
|
|
|
Hurtson
Newbie

 Offline Offline
Activity: 18
Merit: 1

|
 |
September 03, 2019, 02:18:20 PM |
|
Kangaroo System, test friends.
Can you share your scan time and speed?
and How many bits?
I'm
48 bit - 110k / s - 87 sec
51 bit - 110k / s - 200 sec
[################################################]
[# ECDSA Pollard-kangaroo PrivKey Recovery Tool #]
[# based on code by 57fe 2019 #]
[# singlecore #]
[################################################]
[date] Tue Sep 3 17:52:34 2019
[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]
[PRNGseed] 439144377
[bits] 2^50
[i] pubkey#50 loaded from default table
[prvkey#50] 0x00000000000000000000000000000000000000000000000000022bd43c2e9354
[pubkey#50] 03f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6
[format] compressed
[Xcoordinate] f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6
[Ycoordinate] eb3dfcc04c320b55c529291478550be6072977c0c86603fb2e4f5283631064fb
[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]
[+] P-table ready
[~~~~~~~~~~~~~~~~~~~~~~~[1]~~~~~~~~~~~~~~~~~~~~~~]
[+] T+W ready
[~] 144975.9 j/s
[prvkeyX] 00000000000000000000000000000000000000000000000000022bd43c2e9354
[prvkey0] 00000000000000000000000000000000000000000000000000022bd43c2e9354
[double-check] success!
[jump] 82359278
[time] 570.5 sec what i don't understand is , if 2^50 bit address can be found in 570 second. then why, we can't find 2^105 bits of puzzle address in 1140 second? or bit more? but why it takes so much time than it should simply do... |
|
|
|
|
PietCoin97
Jr. Member

 Offline Offline
Activity: 91
Merit: 3

|
 |
September 03, 2019, 03:25:43 PM |
|
#!/usr/bin/python
# by 57fe (fe57.org/forum/thread.php?board=4&thema=1#1)
#######################
# print() compatibility python 2/3
from __future__ import print_function
#######################
# settings
pow2pubkey = 32 # bits/order/pow2/exp key
pow2kangaroo = 3 # discriminator
Ntimeit = 10 # times for avg runtime
prngseed = 0 # 0,any
flag_debug = 0 # 0,1,2,3
#######################
# low order pubkeys
pubkeys = {
16: ('029d8c5d35231d75eb87fd2c5f05f65281ed9573dc41853288c62ee94eb2590b7a', 0xc936)
, 24: ('036ea839d22847ee1dce3bfc5b11f6cf785b0682db58c35b63d1342eb221c3490c', 0xdc2a04)
, 32: ('0209c58240e50e3ba3f833c82655e8725c037a2294e14cf5d73a5df8d56159de69', 0xb862a62e)
, 33: ('02ed949eaca31df5e8be9bf46adc1dfae1734b8900dcc303606831372955c728da', False) #0x01abcd1234
, 40: ('03a2efa402fd5268400c77c20e574ba86409ededee7c4020e4b9f0edbee53de0d4', 0xe9ae4933d6)
, 45: ('026ecabd2d22fdb737be21975ce9a694e108eb94f3649c586cc7461c8abf5da71a', 0x122fca143c05)
, 50: ('03f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6', 0x022bd43c2e9354)
, 65: ('0230210c23b1a047bc9bdbb13448e67deddc108946de6de639bcc75d47c0216b1b', 0x01a838b13505b26867)
,105: ('03bcf7ce887ffca5e62c9cabbdb7ffa71dc183c52c04ff4ee5ee82e0c55c39d77b', False)
}
#######################
# import
import os
import sys
import time
import random
try:
# https://www.lfd.uci.edu/~gohlke/pythonlibs/
import gmpy2
except:
flag_gmpy2 = False
print("[warn] gmpy2 not found. raw python is slow!")
else:
flag_gmpy2 = True
try:
from coincurve import PrivateKey, PublicKey
from coincurve.utils import int_to_bytes, hex_to_bytes, bytes_to_int, bytes_to_hex, int_to_bytes_padded
except:
flag_coincurve = False
#print("[warn] coincurve not found. random pubkey not available!")
else:
flag_coincurve = True
if 0:
from multiprocessing import Pool
from multiprocessing import cpu_count
from multiprocessing import freeze_support
#######################
# python 2,3
#import sys
#import time
if sys.version_info[0] == 2:
from time import clock
else:
from time import perf_counter
from time import process_time
clock = time.perf_counter
xrange=range
raw_input=input
#######################
# secp256k1
#modulo = 2**256-2**32-2**9-2**8-2**7-2**6-2**4-1
modulo = 115792089237316195423570985008687907853269984665640564039457584007908834671663
order = 115792089237316195423570985008687907852837564279074904382605163141518161494337
#modulo = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F
#order = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141
Gx = 55066263022277343669578718895168534326250603453777594175500187360389116729240
Gy = 32670510020758816978083085130507043184471273380659243275938904335757337482424
#Gx = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798
#Gy = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
class Point:
def __init__(self, x=0, y=0):
self.x = x
self.y = y
Gp = Point(Gx,Gy)
Zp = Point(0,0) # zero-point, infinite in real x,y - plane
#######################
# functions
# return (g, x, y) a*x + b*y = gcd(x, y)
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, x, y = egcd(b % a, a)
return (g, y - (b // a) * x, x)
def rev(b, n=modulo):
while b < 0:
b += n
g, x, _ = egcd(b, n)
if g == 1:
return x % n
def mul2(P, p=modulo):
R = Point()
if flag_gmpy2:
c = 3 * P.x * P.x * gmpy2.invert(2*P.y, p) % p
else:
c = 3 * P.x * P.x * rev(2*P.y, p) % p
R.x = (c*c - 2*P.x) % p
R.y = (c*(P.x - R.x) - P.y) % p
return R
# 1I, 3M
def add(P, Q, p=modulo):
R = Point()
dx = Q.x - P.x
dy = Q.y - P.y
if flag_gmpy2: # 1I, 1M
c = dy * gmpy2.invert(dx, p) % p
else:
c = dy * rev(dx, p) % p
R.x = (c*c - P.x - Q.x) % p # 1M
R.y = (c*(P.x - R.x) - P.y) % p # 1M
return R
def mulk(k, P=Gp, p=modulo):
if k == 0: return Zp
elif k == 1: return P
elif (k % 2 == 0):
return mulk(k/2, mul2(P, p), p)
else:
return add(P, mulk( (k-1)/2, mul2(P, p), p), p)
def newX2Y(X, y_parity):
p = modulo
Y = 3
tmp = 1
while Y:
if Y & 1:
tmp = tmp*X % p
Y >>= 1
X = X*X % p
X = (tmp+7) % p
Y = (p+1)//4
tmp = 1
while Y:
if Y & 1:
tmp = tmp*X % p
Y >>= 1
X = X*X % p
Y = tmp
if Y%2 != y_parity:
Y = -Y % p
return Y
def KANGAROO():
DP_rarity = 1 << ((pow2pubkey - 2*pow2kangaroo)//2 - 2)
if flag_debug > 0:
print("[DP_rarity] 1<<((pow2pub - 2*pow2k) -2) = 1<<((%s-2*%s)//2 -2) = %s" % (pow2pubkey,pow2kangaroo,DP_rarity))
jump_modulo = ((pow2pubkey-1) // 2) + pow2kangaroo
if flag_debug > 0:
print("[jump_modulo] (pow2pub-1)//2 + pow2k = (%s-1)//2 + %s = %s" % (pow2pubkey,pow2kangaroo,jump_modulo))
T, t, dt = [], [], []
W, w, dw = [], [], []
if flag_debug > 0:
print( '[t] 3<<(pow2pub-2) + rng(1,(1<<(pow2pub-1))) = 3<<(%s-2) + rng(1,(1<<(%s-1))) = %s + %s' %
( pow2pubkey, pow2pubkey
,3<<(pow2pubkey-2), random.randint(1, (1<<(pow2pubkey-1)))
)
)
for k in range(Nt):
t.append((3 << (pow2pubkey - 2)) + random.randint(1, (1 << (pow2pubkey - 1))))#-(1 << (pow2pubkey - 2)) )
T.append(mulk(t[k]))
dt.append(0)
for k in range(Nw):
w.append(random.randint(1, (1 << (pow2pubkey - 1))))
W.append(add(W0,mulk(w[k])))
dw.append(0)
print('[+] T+W ready')
n_jump = last_jump = 0
prvkey = False;
A, Ak, B, Bk = [], [], [], []
t0 = t1 = t2 = time.time()
while (1):
if flag_debug > 2: print('[new_loop] %s jumps'%n_jump)
for k in range(Nt):
if flag_debug > 2: print('[k/Nt] %s/%s'%(k+1,Nt))
n_jump += 1
pw = T[k].x % jump_modulo
pw = int(pw)
dt[k] = 1 << pw
if T[k].x % (DP_rarity) == 0:
A.append(T[k].x)
Ak.append(t[k])
if flag_debug > 1:
print('[tame] A=%s, B=%s'%(len(A),len(B)))
if flag_debug > 0:
save2file('tame.txt', 'a', '%064x %s\n'%(T[k].x,t[k]) )
result = list(set(A) & set(B))
if len(result) > 0:
sol_kt = A.index(result[0])
sol_kw = B.index(result[0])
prvkey = Ak[sol_kt] - Bk[sol_kw]
if prvkey: break
t[k] += dt[k]
T[k] = add(P[pw], T[k])
if prvkey: break
for k in range(Nw):
if flag_debug > 2: print('[k/Nw] %s/%s'%(k+1,Nw))
n_jump += 1
pw = W[k].x % jump_modulo
pw = int(pw)
dw[k] = 1 << pw
if W[k].x % (DP_rarity) == 0:
B.append(W[k].x)
Bk.append(w[k])
if flag_debug > 1:
print('[wild] A=%s, B=%s'%(len(A),len(B)))
if flag_debug > 0:
save2file('wild.txt', 'a', '%064x %s\n'%(W[k].x,w[k]) )
result = list(set(A) & set(B))
if len(result) > 0:
sol_kt = A.index(result[0])
sol_kw = B.index(result[0])
prvkey = Ak[sol_kt] - Bk[sol_kw]
if prvkey: break
w[k] += dw[k]
W[k] = add(P[pw], W[k])
if prvkey: break
t2 = time.time()
if (t2-t1) > 1:
if sys.version_info[0] == 2:
print('\r[~] %.1f j/s'%((n_jump-last_jump)/(t2-t1)), end='')
sys.stdout.flush()
else:
print('\r[~] %.1f j/s'%((n_jump-last_jump)/(t2-t1)), end='', flush=True )
t1 = t2
last_jump = n_jump
return prvkey, n_jump, (time.time()-t0)
def save2file(path, mode, data):
fp = open(path, mode)
if type(data) in (list,tuple,dict):
fp.writelines(data)
else:
#elif type(data) in (str,int):
fp.write(data)
fp.close()
def usage():
print('[usage] %s [bits] [pubkey]'%(sys.argv[0]))
print(' %s 32'%(sys.argv[0]))
print(' %s 32 %s'%(sys.argv[0],pubkeys[32][0]))
exit(-1)
#######################
#main
if __name__ == '__main__':
#print('[os] %s' % os.name)
if os.name == 'nt':
#freeze_support()
pass
print("[################################################]")
print("[# ECDSA Pollard-kangaroo PrivKey Recovery Tool #]")
print("[# based on code by 57fe 2019 #]")
print("[# singlecore #]");
#print("[# multicore #]");
print("[################################################]")
if len(sys.argv) > 1 and str(sys.argv[1]) in ('--help','-h','/?') :
usage()
print('[date] {}'.format(time.ctime()))
print("[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]")
if prngseed in (0,'0',False,'False','false',''):
prngseed = random.randint(1,2**32)
random.seed(prngseed)
print('[PRNGseed] %s' % prngseed)
if len(sys.argv) > 1 :
try:
pow2pubkey=int(sys.argv[1])
except:
usage()
if pow2pubkey < 1 or pow2pubkey > 256 :
print("[error] bits must be in range 1..256!")
usage()
print('[bits] 2^%s %s' % (pow2pubkey, '(warn: too big!)' if pow2pubkey>50 else ''))
if len(sys.argv) > 2 :
prvkey0 = False
pubkey0 = str(sys.argv[2])
print('[i] pubkey#%s loaded from argv2' % pow2pubkey)
elif flag_coincurve:
prvkey0 = random.randint(1,2**pow2pubkey)
pubkey0 = bytes_to_hex(PublicKey.from_secret(int_to_bytes_padded(prvkey0)).format(1))
#pubkey0 = bytes_to_hex(PublicKey.from_secret(int_to_bytes_padded(prvkey0)).format(0))
print('[i] pubkey#%s randomly generated' % pow2pubkey)
else:
pubkey0, prvkey0 = pubkeys[pow2pubkey]
print('[i] pubkey#%s loaded from default table' % pow2pubkey)
else:
print('[bits] 2^%s %s' % (pow2pubkey, '(warn: too big!)' if pow2pubkey>50 else ''))
pubkey0, prvkey0 = pubkeys[pow2pubkey]
print('[i] pubkey#%s loaded from default table' % pow2pubkey)
if prvkey0 not in (0,'0',False,'False','false',''):
print('[prvkey#%s] 0x%064x' % (pow2pubkey,prvkey0))
print('[pubkey#%s] %s' % (pow2pubkey,pubkey0))
#calc Y if pubkey is compress
if len(pubkey0)==130:
X = int(pubkey0[2:66], 16)
Y = int(pubkey0[66:],16)
print("[format] uncompressed")
elif len(pubkey0)==66:
X = int(pubkey0[2:66], 16)
Y = newX2Y(X,int(pubkey0[:2])-2)
print("[format] compressed")
else:
print("[error] pubkey len(66/130) invalid!")
usage()
print("[Xcoordinate] %064x" % X)
print("[Ycoordinate] %064x" % Y)
W0 = Point(X,Y)
print("[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~]")
starttime = time.time()
P = [Gp]
for k in range(255): P.append(mul2(P[k]))
print('[+] P-table ready')
Nt = Nw = 2**pow2kangaroo
if flag_debug > 0:
print("[range(L..U)] 1..2^%s(0x%x)" % (pow2pubkey, 2**pow2pubkey))
print("[w=U-L] 0x%x ; w/2=0x%x" % (2**pow2pubkey, 2**(pow2pubkey-1)))
print("[pow2k] 2^%s: Nt=%s, Nw=%s" % (pow2kangaroo,Nt,Nw))
jumps_list = []
runtime_list = []
#timeit
for i in range(Ntimeit):
print("[~~~~~~~~~~~~~~~~~~~~~~~[%s]~~~~~~~~~~~~~~~~~~~~~~]"%(i+1))
if flag_debug > 0:
save2file('tame.txt', 'w', '')
save2file('wild.txt', 'w', '')
prvkey, n_jump, runtime = KANGAROO()
jumps_list.append(n_jump)
runtime_list.append(runtime)
print('')
print('[prvkeyX] %064x' % (prvkey) )
save2file('results.txt', 'a', ('%064x\n'%prvkey, '---------------\n'))
if prvkey0 not in (0,'0',False,'False','false',''):
print('[prvkey0] %064x' % (prvkey0))
if prvkey == prvkey0:
print('[double-check] success!')
else:
print('[double-check] failed!')
print('[jump] %s' % n_jump)
print('[time] %.1f sec' % runtime)
print("[################################################]")
if Ntimeit > 1:
M = sum(jumps_list)*1.0 / len(jumps_list)
print('[(avg)jump] %.0f' % (M) )
#D = sum((xi - M) ** 2 for xi in jumps_list)*1.0 / len(jumps_list)
#print('[(avg)jum2] %.1f +/- %.1f' % (M, (D/(len(jumps_list)-1))**0.5) )
print('[(avg)time] %.1f sec' % (sum(runtime for runtime in runtime_list)/Ntimeit) )
#print('[(avg)tim2] %.1f sec' % ((time.time()-starttime)/Ntimeit) )
else:
pass
print("[################################################]")
print('[date] {}'.format(time.ctime()))
#print('[exit] exit')
#print('');raw_input('Press ENTER to continue...');print('')
exit(0)
Addon needed remove pubkeys = xxxxxx add example ** with open("pubkeys.txt", "r") as m: add = m.read().split() for ad in add: *** multi pubkeys at once check inside bit range this script check only 1 pubkey in bit range yeah this would be very interesting the chance to find somethiong is much higher than to search only for one you have to know we know the most pub key from the first mining reward addresses more then 70k pub keys maybe most of them are in bit space 250 to 256 but would it work does someone a test if multiple pub keys work ? |
|
|
|
|
racminer
Member
 
 Offline Offline
Activity: 242
Merit: 17

|
 |
September 04, 2019, 01:08:27 AM
Last edit: September 04, 2019, 02:33:34 AM by racminer |
|
This is a continuation of the popular "32 btc puzzle" ( https://bitcointalk.org/index.php?topic=1306983.0) topic with the inclusion of the latest data updated. ............................. ............................. No. |=========PRIVATE KEY IN HEX (if it was found and known)========== |===========WALLET ADDRESS===========| ===============UPPER RANGE LIMIT================ | ===================COMPRESSED PUBLIC KEY IN HEX=================== | ==SOLVED DATE==
01 | 0000000000000000000000000000000000000000000000000000000000000001 | 1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH | 1 | 0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798 | 2015-01-15
02 | 0000000000000000000000000000000000000000000000000000000000000003 | 1CUNEBjYrCn2y1SdiUMohaKUi4wpP326Lb | 3 | 02f9308a019258c31049344f85f89d5229b531c845836f99b08601f113bce036f9 | 2015-01-15
03 | 0000000000000000000000000000000000000000000000000000000000000007 | 19ZewH8Kk1PDbSNdJ97FP4EiCjTRaZMZQA | 7 | 025cbdf0646e5db4eaa398f365f2ea7a0e3d419b7e0330e39ce92bddedcac4f9bc | 2015-01-15
04 | 0000000000000000000000000000000000000000000000000000000000000008 | 1EhqbyUMvvs7BfL8goY6qcPbD6YKfPqb7e | 15 | 022f01e5e15cca351daff3843fb70f3c2f0a1bdd05e5af888a67784ef3e10a2a01 | 2015-01-15
05 | 0000000000000000000000000000000000000000000000000000000000000015 | 1E6NuFjCi27W5zoXg8TRdcSRq84zJeBW3k | 31 | 02352bbf4a4cdd12564f93fa332ce333301d9ad40271f8107181340aef25be59d5 | 2015-01-15
06 | 0000000000000000000000000000000000000000000000000000000000000031 | 1PitScNLyp2HCygzadCh7FveTnfmpPbfp8 | 63 | 03f2dac991cc4ce4b9ea44887e5c7c0bce58c80074ab9d4dbaeb28531b7739f530 | 2015-01-15
07 | 000000000000000000000000000000000000000000000000000000000000004C | 1McVt1vMtCC7yn5b9wgX1833yCcLXzueeC | 127 | 0296516a8f65774275278d0d7420a88df0ac44bd64c7bae07c3fe397c5b3300b23 | 2015-01-15
08 | 00000000000000000000000000000000000000000000000000000000000000E0 | 1M92tSqNmQLYw33fuBvjmeadirh1ysMBxK | 255 | 0308bc89c2f919ed158885c35600844d49890905c79b357322609c45706ce6b514 | 2015-01-15
09 | 00000000000000000000000000000000000000000000000000000000000001D3 | 1CQFwcjw1dwhtkVWBttNLDtqL7ivBonGPV | 511 | 0243601d61c836387485e9514ab5c8924dd2cfd466af34ac95002727e1659d60f7 | 2015-01-15
10 | 0000000000000000000000000000000000000000000000000000000000000202 | 1LeBZP5QCwwgXRtmVUvTVrraqPUokyLHqe | 1023 | 03a7a4c30291ac1db24b4ab00c442aa832f7794b5a0959bec6e8d7fee802289dcd | 2015-01-15
11 | 0000000000000000000000000000000000000000000000000000000000000483 | 1PgQVLmst3Z314JrQn5TNiys8Hc38TcXJu | 2047 | 038b05b0603abd75b0c57489e451f811e1afe54a8715045cdf4888333f3ebc6e8b | 2015-01-15
12 | 0000000000000000000000000000000000000000000000000000000000000A7B | 1DBaumZxUkM4qMQRt2LVWyFJq5kDtSZQot | 4095 | 038b00fcbfc1a203f44bf123fc7f4c91c10a85c8eae9187f9d22242b4600ce781c | 2015-01-15
13 | 0000000000000000000000000000000000000000000000000000000000001460 | 1Pie8JkxBT6MGPz9Nvi3fsPkr2D8q3GBc1 | 8191 | 03aadaaab1db8d5d450b511789c37e7cfeb0eb8b3e61a57a34166c5edc9a4b869d | 2015-01-15
14 | 0000000000000000000000000000000000000000000000000000000000002930 | 1ErZWg5cFCe4Vw5BzgfzB74VNLaXEiEkhk | 16383 | 03b4f1de58b8b41afe9fd4e5ffbdafaeab86c5db4769c15d6e6011ae7351e54759 | 2015-01-15
15 | 00000000000000000000000000000000000000000000000000000000000068F3 | 1QCbW9HWnwQWiQqVo5exhAnmfqKRrCRsvW | 32767 | 02fea58ffcf49566f6e9e9350cf5bca2861312f422966e8db16094beb14dc3df2c | 2015-01-15
16 | 000000000000000000000000000000000000000000000000000000000000C936 | 1BDyrQ6WoF8VN3g9SAS1iKZcPzFfnDVieY | 65535 | 029d8c5d35231d75eb87fd2c5f05f65281ed9573dc41853288c62ee94eb2590b7a | 2015-01-15
17 | 000000000000000000000000000000000000000000000000000000000001764F | 1HduPEXZRdG26SUT5Yk83mLkPyjnZuJ7Bm | 131071 | 033f688bae8321b8e02b7e6c0a55c2515fb25ab97d85fda842449f7bfa04e128c3 | 2015-01-15
18 | 000000000000000000000000000000000000000000000000000000000003080D | 1GnNTmTVLZiqQfLbAdp9DVdicEnB5GoERE | 262143 | 020ce4a3291b19d2e1a7bf73ee87d30a6bdbc72b20771e7dfff40d0db755cd4af1 | 2015-01-15
19 | 000000000000000000000000000000000000000000000000000000000005749F | 1NWmZRpHH4XSPwsW6dsS3nrNWfL1yrJj4w | 524287 | 0385663c8b2f90659e1ccab201694f4f8ec24b3749cfe5030c7c3646a709408e19 | 2015-01-15
20 | 00000000000000000000000000000000000000000000000000000000000D2C55 | 1HsMJxNiV7TLxmoF6uJNkydxPFDog4NQum | 1048575 | 033c4a45cbd643ff97d77f41ea37e843648d50fd894b864b0d52febc62f6454f7c | 2015-01-15
21 | 00000000000000000000000000000000000000000000000000000000001BA534 | 14oFNXucftsHiUMY8uctg6N487riuyXs4h | 2097151 | 031a746c78f72754e0be046186df8a20cdce5c79b2eda76013c647af08d306e49e | 2015-01-15
22 | 00000000000000000000000000000000000000000000000000000000002DE40F | 1CfZWK1QTQE3eS9qn61dQjV89KDjZzfNcv | 4194303 | 023ed96b524db5ff4fe007ce730366052b7c511dc566227d929070b9ce917abb43 | 2015-01-15
23 | 0000000000000000000000000000000000000000000000000000000000556E52 | 1L2GM8eE7mJWLdo3HZS6su1832NX2txaac | 8388607 | 03f82710361b8b81bdedb16994f30c80db522450a93e8e87eeb07f7903cf28d04b | 2015-01-15
24 | 0000000000000000000000000000000000000000000000000000000000DC2A04 | 1rSnXMr63jdCuegJFuidJqWxUPV7AtUf7 | 16777215 | 036ea839d22847ee1dce3bfc5b11f6cf785b0682db58c35b63d1342eb221c3490c | 2015-01-15
25 | 0000000000000000000000000000000000000000000000000000000001FA5EE5 | 15JhYXn6Mx3oF4Y7PcTAv2wVVAuCFFQNiP | 33554431 | 03057fbea3a2623382628dde556b2a0698e32428d3cd225f3bd034dca82dd7455a | 2015-01-15
26 | 000000000000000000000000000000000000000000000000000000000340326E | 1JVnST957hGztonaWK6FougdtjxzHzRMMg | 67108863 | 024e4f50a2a3eccdb368988ae37cd4b611697b26b29696e42e06d71368b4f3840f | 2015-01-15
27 | 0000000000000000000000000000000000000000000000000000000006AC3875 | 128z5d7nN7PkCuX5qoA4Ys6pmxUYnEy86k | 134217727 | 031a864bae3922f351f1b57cfdd827c25b7e093cb9c88a72c1cd893d9f90f44ece | 2015-01-15
28 | 000000000000000000000000000000000000000000000000000000000D916CE8 | 12jbtzBb54r97TCwW3G1gCFoumpckRAPdY | 268435455 | 03e9e661838a96a65331637e2a3e948dc0756e5009e7cb5c36664d9b72dd18c0a7 | 2015-01-16
29 | 0000000000000000000000000000000000000000000000000000000017E2551E | 19EEC52krRUK1RkUAEZmQdjTyHT7Gp1TYT | 536870911 | 026caad634382d34691e3bef43ed4a124d8909a8a3362f91f1d20abaaf7e917b36 | 2015-01-16
30 | 000000000000000000000000000000000000000000000000000000003D94CD64 | 1LHtnpd8nU5VHEMkG2TMYYNUjjLc992bps | 1073741823 | 030d282cf2ff536d2c42f105d0b8588821a915dc3f9a05bd98bb23af67a2e92a5b | 2015-01-16
31 | 000000000000000000000000000000000000000000000000000000007D4FE747 | 1LhE6sCTuGae42Axu1L1ZB7L96yi9irEBE | 2147483647 | 0387dc70db1806cd9a9a76637412ec11dd998be666584849b3185f7f9313c8fd28 | 2015-01-16
32 | 00000000000000000000000000000000000000000000000000000000B862A62E | 1FRoHA9xewq7DjrZ1psWJVeTer8gHRqEvR | 4294967295 | 0209c58240e50e3ba3f833c82655e8725c037a2294e14cf5d73a5df8d56159de69 | 2015-01-16
33 | 00000000000000000000000000000000000000000000000000000001A96CA8D8 | 187swFMjz1G54ycVU56B7jZFHFTNVQFDiu | 8589934591 | 03a355aa5e2e09dd44bb46a4722e9336e9e3ee4ee4e7b7a0cf5785b283bf2ab579 | 2015-01-17
34 | 000000000000000000000000000000000000000000000000000000034A65911D | 1PWABE7oUahG2AFFQhhvViQovnCr4rEv7Q | 17179869183 | 033cdd9d6d97cbfe7c26f902faf6a435780fe652e159ec953650ec7b1004082790 | 2015-01-17
35 | 00000000000000000000000000000000000000000000000000000004AED21170 | 1PWCx5fovoEaoBowAvF5k91m2Xat9bMgwb | 34359738367 | 02f6a8148a62320e149cb15c544fe8a25ab483a0095d2280d03b8a00a7feada13d | 2015-01-17
36 | 00000000000000000000000000000000000000000000000000000009DE820A7C | 1Be2UF9NLfyLFbtm3TCbmuocc9N1Kduci1 | 68719476735 | 02b3e772216695845fa9dda419fb5daca28154d8aa59ea302f05e916635e47b9f6 | 2015-01-18
37 | 0000000000000000000000000000000000000000000000000000001757756A93 | 14iXhn8bGajVWegZHJ18vJLHhntcpL4dex | 137438953471 | 027d2c03c3ef0aec70f2c7e1e75454a5dfdd0e1adea670c1b3a4643c48ad0f1255 | 2015-01-19
38 | 00000000000000000000000000000000000000000000000000000022382FACD0 | 1HBtApAFA9B2YZw3G2YKSMCtb3dVnjuNe2 | 274877906943 | 03c060e1e3771cbeccb38e119c2414702f3f5181a89652538851d2e3886bdd70c6 | 2015-01-21
39 | 0000000000000000000000000000000000000000000000000000004B5F8303E9 | 122AJhKLEfkFBaGAd84pLp1kfE7xK3GdT8 | 549755813887 | 022d77cd1467019a6bf28f7375d0949ce30e6b5815c2758b98a74c2700bc006543 | 2015-01-30
40 | 000000000000000000000000000000000000000000000000000000E9AE4933D6 | 1EeAxcprB2PpCnr34VfZdFrkUWuxyiNEFv | 1099511627775 | 03a2efa402fd5268400c77c20e574ba86409ededee7c4020e4b9f0edbee53de0d4 | 2015-01-30
41 | 00000000000000000000000000000000000000000000000000000153869ACC5B | 1L5sU9qvJeuwQUdt4y1eiLmquFxKjtHr3E | 2199023255551 | 03b357e68437da273dcf995a474a524439faad86fc9effc300183f714b0903468b | 2015-01-30
42 | 000000000000000000000000000000000000000000000000000002A221C58D8F | 1E32GPWgDyeyQac4aJxm9HVoLrrEYPnM4N | 4398046511103 | 03eec88385be9da803a0d6579798d977a5d0c7f80917dab49cb73c9e3927142cb6 | 2015-01-30
43 | 000000000000000000000000000000000000000000000000000006BD3B27C591 | 1PiFuqGpG8yGM5v6rNHWS3TjsG6awgEGA1 | 8796093022207 | 02a631f9ba0f28511614904df80d7f97a4f43f02249c8909dac92276ccf0bcdaed | 2015-01-30 ( )
44 | 00000000000000000000000000000000000000000000000000000E02B35A358F | 1CkR2uS7LmFwc3T2jV8C1BhWb5mQaoxedF | 17592186044415 | 025e466e97ed0e7910d3d90ceb0332df48ddf67d456b9e7303b50a3d89de357336 | 2015-01-30
45 | 0000000000000000000000000000000000000000000000000000122FCA143C05 | 1NtiLNGegHWE3Mp9g2JPkgx6wUg4TW7bbk | 35184372088831 | 026ecabd2d22fdb737be21975ce9a694e108eb94f3649c586cc7461c8abf5da71a | 2015-01-30
46 | 00000000000000000000000000000000000000000000000000002EC18388D544 | 1F3JRMWudBaj48EhwcHDdpeuy2jwACNxjP | 70368744177663 | 03fd5487722d2576cb6d7081426b66a3e2986c1ce8358d479063fb5f2bb6dd5849 | 2015-09-01
47 | 00000000000000000000000000000000000000000000000000006CD610B53CBA | 1Pd8VvT49sHKsmqrQiP61RsVwmXCZ6ay7Z | 140737488355327 | 023a12bd3caf0b0f77bf4eea8e7a40dbe27932bf80b19ac72f5f5a64925a594196 | 2015-09-01
48 | 0000000000000000000000000000000000000000000000000000ADE6D7CE3B9B | 1DFYhaB2J9q1LLZJWKTnscPWos9VBqDHzv | 281474976710655 | 0291bee5cf4b14c291c650732faa166040e4c18a14731f9a930c1e87d3ec12debb | 2015-09-01
49 | 000000000000000000000000000000000000000000000000000174176B015F4D | 12CiUhYVTTH33w3SPUBqcpMoqnApAV4WCF | 562949953421311 | 02591d682c3da4a2a698633bf5751738b67c343285ebdc3492645cb44658911484 | 2015-09-01
50 | 00000000000000000000000000000000000000000000000000022BD43C2E9354 | 1MEzite4ReNuWaL5Ds17ePKt2dCxWEofwk | 1125899906842623 | 03f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6 | 2017-04-05
51 | 00000000000000000000000000000000000000000000000000075070A1A009D4 | 1NpnQyZ7x24ud82b7WiRNvPm6N8bqGQnaS | 2251799813685247 | 028c6c67bef9e9eebe6a513272e50c230f0f91ed560c37bc9b033241ff6c3be78f | 2017-04-21
52 | 000000000000000000000000000000000000000000000000000EFAE164CB9E3C | 15z9c9sVpu6fwNiK7dMAFgMYSK4GqsGZim | 4503599627370495 | 0374c33bd548ef02667d61341892134fcf216640bc2201ae61928cd0874f6314a7 | 2017-09-04
53 | 00000000000000000000000000000000000000000000000000180788E47E326C | 15K1YKJMiJ4fpesTVUcByoz334rHmknxmT | 9007199254740991 | 020faaf5f3afe58300a335874c80681cf66933e2a7aeb28387c0d28bb048bc6349 | 2017-09-04
54 | 00000000000000000000000000000000000000000000000000236FB6D5AD1F43 | 1KYUv7nSvXx4642TKeuC2SNdTk326uUpFy | 18014398509481983 | 034af4b81f8c450c2c870ce1df184aff1297e5fcd54944d98d81e1a545ffb22596 | 2017-11-16
55 | 000000000000000000000000000000000000000000000000006ABE1F9B67E114 | 1LzhS3k3e9Ub8i2W1V8xQFdB8n2MYCHPCa | 36028797018963967 | 0385a30d8413af4f8f9e6312400f2d194fe14f02e719b24c3f83bf1fd233a8f963 | 2018-05-29
56 | 000000000000000000000000000000000000000000000000009D18B63AC4FFDF | 17aPYR1m6pVAacXg1PTDDU7XafvK1dxvhi | 72057594037927935 | 033f2db2074e3217b3e5ee305301eeebb1160c4fa1e993ee280112f6348637999a | 2018-09-08
57 | 00000000000000000000000000000000000000000000000001EB25C90795D61C | 15c9mPGLku1HuW9LRtBf4jcHVpBUt8txKz | 144115188075855871 | 02a521a07e98f78b03fc1e039bc3a51408cd73119b5eb116e583fe57dc8db07aea | 2018-11-08
58 | 00000000000000000000000000000000000000000000000002C675B852189A21 | 1Dn8NF8qDyyfHMktmuoQLGyjWmZXgvosXf | 288230376151711743 | 0311569442e870326ceec0de24eb5478c19e146ecd9d15e4666440f2f638875f42 | 2018-12-03
59 | 00000000000000000000000000000000000000000000000007496CBB87CAB44F | 1HAX2n9Uruu9YDt4cqRgYcvtGvZj1rbUyt | 576460752303423487 | 0241267d2d7ee1a8e76f8d1546d0d30aefb2892d231cee0dde7776daf9f8021485 | 2019-02-11
60 | 0000000000000000000000000000000000000000000000000FC07A1825367BBE | 1Kn5h2qpgw9mWE5jKpk8PP4qvvJ1QVy8su | 1152921504606846975 | 0348e843dc5b1bd246e6309b4924b81543d02b16c8083df973a89ce2c7eb89a10d | 2019-02-17
61 | 00000000000000000000000000000000000000000000000013C96A3742F64906 | 1AVJKwzs9AskraJLGHAZPiaZcrpDr1U6AB | 2305843009213693951 | 0249a43860d115143c35c09454863d6f82a95e47c1162fb9b2ebe0186eb26f453f | 2019-05-11
62 | | 1Me6EfpwZK5kQziBwBfvLiHjaPGxCKLoJi | 4611686018427387903 |
63 | 0000000000000000000000000000000000000000000000007CCE5EFDACCF6808 | 1NpYjtLira16LfGbGwZJ5JbDPh3ai9bjf4 | 9223372036854775807 | 0365ec2994b8cc0a20d40dd69edfe55ca32a54bcbbaa6b0ddcff36049301a54579 | 2019-06-07 (zielar)
64 | | 16jY7qLJnxb7CHZyqBP8qca9d51gAjyXQN | 18446744073709551615 |
65 | 000000000000000000000000000000000000000000000001A838B13505B26867 | 18ZMbwUFLMHoZBbfpCjUJQTCMCbktshgpe | 36893488147419103231 | 0230210c23b1a047bc9bdbb13448e67deddc108946de6de639bcc75d47c0216b1b | 2019-06-07
66 | | 13zb1hQbWVsc2S7ZTZnP2G4undNNpdh5so | 73786976294838206463 |
67 | | 1BY8GQbnueYofwSuFAT3USAhGjPrkxDdW9 | 147573952589676412927 |
68 | | 1MVDYgVaSN6iKKEsbzRUAYFrYJadLYZvvZ | 295147905179352825855 |
69 | | 19vkiEajfhuZ8bs8Zu2jgmC6oqZbWqhxhG | 590295810358705651711 |
70 | 0000000000000000000000000000000000000000000000349B84B6431A6C4EF1 | 19YZECXj3SxEZMoUeJ1yiPsw8xANe7M7QR | 1180591620717411303423 | 0290e6900a58d33393bc1097b5aed31f2e4e7cbd3e5466af958665bc0121248483 | 2019-06-09
71 | | 1PWo3JeB9jrGwfHDNpdGK54CRas7fsVzXU | 2361183241434822606847 |
72 | | 1JTK7s9YVYywfm5XUH7RNhHJH1LshCaRFR | 4722366482869645213695 |
73 | | 12VVRNPi4SJqUTsp6FmqDqY5sGosDtysn4 | 9444732965739290427391 |
74 | | 1FWGcVDK3JGzCC3WtkYetULPszMaK2Jksv | 18889465931478580854783 |
75 | 0000000000000000000000000000000000000000000004C5CE114686A1336E07 | 1J36UjUByGroXcCvmj13U6uwaVv9caEeAt | 37778931862957161709567 | 03726b574f193e374686d8e12bc6e4142adeb06770e0a2856f5e4ad89f66044755 | 2019-06-10
76 | | 1DJh2eHFYQfACPmrvpyWc8MSTYKh7w9eRF | 75557863725914323419135 |
77 | | 1Bxk4CQdqL9p22JEtDfdXMsng1XacifUtE | 151115727451828646838271 |
78 | | 15qF6X51huDjqTmF9BJgxXdt1xcj46Jmhb | 302231454903657293676543 |
79 | | 1ARk8HWJMn8js8tQmGUJeQHjSE7KRkn2t8 | 604462909807314587353087 |
80 | 00000000000000000000000000000000000000000000EA1A5C66DCC11B5AD180 | 1BCf6rHUW6m3iH2ptsvnjgLruAiPQQepLe | 1208925819614629174706175 | 037e1238f7b1ce757df94faa9a2eb261bf0aeb9f84dbf81212104e78931c2a19dc | 2019-06-11
81 | | 15qsCm78whspNQFydGJQk5rexzxTQopnHZ | 2417851639229258349412351 |
82 | | 13zYrYhhJxp6Ui1VV7pqa5WDhNWM45ARAC | 4835703278458516698824703 |
83 | | 14MdEb4eFcT3MVG5sPFG4jGLuHJSnt1Dk2 | 9671406556917033397649407 |
84 | | 1CMq3SvFcVEcpLMuuH8PUcNiqsK1oicG2D | 19342813113834066795298815 |
85 | 00000000000000000000000000000000000000000011720C4F018D51B8CEBBA8 | 1Kh22PvXERd2xpTQk3ur6pPEqFeckCJfAr | 38685626227668133590597631 | 0329c4574a4fd8c810b7e42a4b398882b381bcd85e40c6883712912d167c83e73a | 2019-06-17
86 | | 1K3x5L6G57Y494fDqBfrojD28UJv4s5JcK | 77371252455336267181195263 |
87 | | 1PxH3K1Shdjb7gSEoTX7UPDZ6SH4qGPrvq | 154742504910672534362390527 |
88 | | 16AbnZjZZipwHMkYKBSfswGWKDmXHjEpSf | 309485009821345068724781055 |
89 | | 19QciEHbGVNY4hrhfKXmcBBCrJSBZ6TaVt | 618970019642690137449562111 |
90 | 000000000000000000000000000000000000000002CE00BB2136A445C71E85BF | 1L12FHH2FHjvTviyanuiFVfmzCy46RRATU | 1237940039285380274899124223 | 035c38bd9ae4b10e8a250857006f3cfd98ab15a6196d9f4dfd25bc7ecc77d788d5 | 2019-07-01
91 | | 1EzVHtmbN4fs4MiNk3ppEnKKhsmXYJ4s74 | 2475880078570760549798248447 |
92 | | 1AE8NzzgKE7Yhz7BWtAcAAxiFMbPo82NB5 | 4951760157141521099596496895 |
93 | | 17Q7tuG2JwFFU9rXVj3uZqRtioH3mx2Jad | 9903520314283042199192993791 |
94 | | 1K6xGMUbs6ZTXBnhw1pippqwK6wjBWtNpL | 19807040628566084398385987583 |
95 | 0000000000000000000000000000000000000000527a792b183c7f64a0e8b1f4 | 19eVSDuizydXxhohGh8Ki9WY9KsHdSwoQC | 39614081257132168796771975167 | 02967a5905d6f3b420959a02789f96ab4c3223a2c4d2762f817b7895c5bc88a045 | 2019-07-06
96 | | 15ANYzzCp5BFHcCnVFzXqyibpzgPLWaD8b | 79228162514264337593543950335 |
97 | | 18ywPwj39nGjqBrQJSzZVq2izR12MDpDr8 | 158456325028528675187087900671 |
98 | | 1CaBVPrwUxbQYYswu32w7Mj4HR4maNoJSX | 316912650057057350374175801343 |
99 | | 1JWnE6p6UN7ZJBN7TtcbNDoRcjFtuDWoNL | 633825300114114700748351602687 |
100 | 000000000000000000000000000000000000000af55fc59c335c8ec67ed24826 | 1KCgMv8fo2TPBpddVi9jqmMmcne9uSNJ5F | 1267650600228229401496703205375 | 03d2063d40402f030d4cc71331468827aa41a8a09bd6fd801ba77fb64f8e67e617 | 2019-07-08
101 | | 1CKCVdbDJasYmhswB6HKZHEAnNaDpK7W4n | 2535301200456458802993406410751 |
102 | | 1PXv28YxmYMaB8zxrKeZBW8dt2HK7RkRPX | 5070602400912917605986812821503 |
103 | | 1AcAmB6jmtU6AiEcXkmiNE9TNVPsj9DULf | 10141204801825835211973625643007 |
104 | | 1EQJvpsmhazYCcKX5Au6AZmZKRnzarMVZu | 20282409603651670423947251286015 |
105 | | 1CMjscKB3QW7SDyQ4c3C3DEUHiHRhiZVib | 40564819207303340847894502572031 | 03bcf7ce887ffca5e62c9cabbdb7ffa71dc183c52c04ff4ee5ee82e0c55c39d77b
106 | | 18KsfuHuzQaBTNLASyj15hy4LuqPUo1FNB | 81129638414606681695789005144063 |
107 | | 15EJFC5ZTs9nhsdvSUeBXjLAuYq3SWaxTc | 162259276829213363391578010288127 |
108 | | 1HB1iKUqeffnVsvQsbpC6dNi1XKbyNuqao | 324518553658426726783156020576255 |
109 | | 1GvgAXVCbA8FBjXfWiAms4ytFeJcKsoyhL | 649037107316853453566312041152511 |
110 | | 12JzYkkN76xkwvcPT6AWKZtGX6w2LAgsJg | 1298074214633706907132624082305023 | 0309976ba5570966bf889196b7fdf5a0f9a1e9ab340556ec29f8bb60599616167d
111 | | 1824ZJQ7nKJ9QFTRBqn7z7dHV5EGpzUpH3 | 2596148429267413814265248164610047 |
112 | | 18A7NA9FTsnJxWgkoFfPAFbQzuQxpRtCos | 5192296858534827628530496329220095 |
113 | | 1NeGn21dUDDeqFQ63xb2SpgUuXuBLA4WT4 | 10384593717069655257060992658440191 |
114 | | 174SNxfqpdMGYy5YQcfLbSTK3MRNZEePoy | 20769187434139310514121985316880383 |
115 | | 1NLbHuJebVwUZ1XqDjsAyfTRUPwDQbemfv | 41538374868278621028243970633760767 | 0248d313b0398d4923cdca73b8cfa6532b91b96703902fc8b32fd438a3b7cd7f55
116 | | 1MnJ6hdhvK37VLmqcdEwqC3iFxyWH2PHUV | 83076749736557242056487941267521535 |
117 | | 1KNRfGWw7Q9Rmwsc6NT5zsdvEb9M2Wkj5Z | 166153499473114484112975882535043071 |
118 | | 1PJZPzvGX19a7twf5HyD2VvNiPdHLzm9F6 | 332306998946228968225951765070086143 |
119 | | 1GuBBhf61rnvRe4K8zu8vdQB3kHzwFqSy7 | 664613997892457936451903530140172287 |
120 | | 17s2b9ksz5y7abUm92cHwG8jEPCzK3dLnT | 1329227995784915872903807060280344575 | 02ceb6cbbcdbdf5ef7150682150f4ce2c6f4807b349827dcdbdd1f2efa885a2630
121 | | 1GDSuiThEV64c166LUFC9uDcVdGjqkxKyh | 2658455991569831745807614120560689151 |
122 | | 1Me3ASYt5JCTAK2XaC32RMeH34PdprrfDx | 5316911983139663491615228241121378303 |
123 | | 1CdufMQL892A69KXgv6UNBD17ywWqYpKut | 10633823966279326983230456482242756607 |
124 | | 1BkkGsX9ZM6iwL3zbqs7HWBV7SvosR6m8N | 21267647932558653966460912964485513215 |
125 | | 1PXAyUB8ZoH3WD8n5zoAthYjN15yN5CVq5 | 42535295865117307932921825928971026431 | 0233709eb11e0d4439a729f21c2c443dedb727528229713f0065721ba8fa46f00e
126 | | 1AWCLZAjKbV1P7AHvaPNCKiB7ZWVDMxFiz | 85070591730234615865843651857942052863 |
127 | | 1G6EFyBRU86sThN3SSt3GrHu1sA7w7nzi4 | 170141183460469231731687303715884105727 |
128 | | 1MZ2L1gFrCtkkn6DnTT2e4PFUTHw9gNwaj | 340282366920938463463374607431768211455 |
129 | | 1Hz3uv3nNZzBVMXLGadCucgjiCs5W9vaGz | 680564733841876926926749214863536422911 |
130 | | 1Fo65aKq8s8iquMt6weF1rku1moWVEd5Ua | 1361129467683753853853498429727072845823 | 03633cbe3ec02b9401c5effa144c5b4d22f87940259634858fc7e59b1c09937852
131 | | 16zRPnT8znwq42q7XeMkZUhb1bKqgRogyy | 2722258935367507707706996859454145691647 |
132 | | 1KrU4dHE5WrW8rhWDsTRjR21r8t3dsrS3R | 5444517870735015415413993718908291383295 |
133 | | 17uDfp5r4n441xkgLFmhNoSW1KWp6xVLD | 10889035741470030830827987437816582766591 |
134 | | 13A3JrvXmvg5w9XGvyyR4JEJqiLz8ZySY3 | 16333553612205046246241981156724874149887 |
135 | | 16RGFo6hjq9ym6Pj7N5H7L1NR1rVPJyw2v | 21778071482940061661655974875633165533183 | 02145d2611c823a396ef6712ce0f712f09b9b4f3135e3e0aa3230fb9b6d08d1e16
136 | | 1UDHPdovvR985NrWSkdWQDEQ1xuRiTALq | 43556142965880123323311949751266331066367 |
137 | | 15nf31J46iLuK1ZkTnqHo7WgN5cARFK3RA | 87112285931760246646623899502532662132735 |
138 | | 1Ab4vzG6wEQBDNQM1B2bvUz4fqXXdFk2WT | 174224571863520493293247799005065324265471 |
139 | | 1Fz63c775VV9fNyj25d9Xfw3YHE6sKCxbt | 348449143727040986586495598010130648530943 |
140 | | 1QKBaU6WAeycb3DbKbLBkX7vJiaS8r42Xo | 696898287454081973172991196020261297061887 | 031f6a332d3c5c4f2de2378c012f429cd109ba07d69690c6c701b6bb87860d6640
141 | | 1CD91Vm97mLQvXhrnoMChhJx4TP9MaQkJo | 1393796574908163946345982392040522594123775 |
142 | | 15MnK2jXPqTMURX4xC3h4mAZxyCcaWWEDD | 2787593149816327892691964784081045188247551 |
143 | | 13N66gCzWWHEZBxhVxG18P8wyjEWF9Yoi1 | 5575186299632655785383929568162090376495103 |
144 | | 1NevxKDYuDcCh1ZMMi6ftmWwGrZKC6j7Ux | 11150372599265311570767859136324180752990207 |
145 | | 19GpszRNUej5yYqxXoLnbZWKew3KdVLkXg | 22300745198530623141535718272648361505980415 | 03afdda497369e219a2c1c369954a930e4d3740968e5e4352475bcffce3140dae5
146 | | 1M7ipcdYHey2Y5RZM34MBbpugghmjaV89P | 44601490397061246283071436545296723011960831 |
147 | | 18aNhurEAJsw6BAgtANpexk5ob1aGTwSeL | 89202980794122492566142873090593446023921663 |
148 | | 1FwZXt6EpRT7Fkndzv6K4b4DFoT4trbMrV | 178405961588244985132285746181186892047843327 |
149 | | 1CXvTzR6qv8wJ7eprzUKeWxyGcHwDYP1i2 | 356811923176489970264571492362373784095686655 |
150 | | 1MUJSJYtGPVGkBCTqGspnxyHahpt5Te8jy | 713623846352979940529142984724747568191373311 | 03137807790ea7dc6e97901c2bc87411f45ed74a5629315c4e4b03a0a102250c49
151 | | 13Q84TNNvgcL3HJiqQPvyBb9m4hxjS3jkV | 1427247692705959881058285969449495136382746623 |
152 | | 1LuUHyrQr8PKSvbcY1v1PiuGuqFjWpDumN | 2854495385411919762116571938898990272765493247 |
153 | | 18192XpzzdDi2K11QVHR7td2HcPS6Qs5vg | 5708990770823839524233143877797980545530986495 |
154 | | 1NgVmsCCJaKLzGyKLFJfVequnFW9ZvnMLN | 11417981541647679048466287755595961091061972991 |
155 | | 1AoeP37TmHdFh8uN72fu9AqgtLrUwcv2wJ | 22835963083295358096932575511191922182123945983 | 035cd1854cae45391ca4ec428cc7e6c7d9984424b954209a8eea197b9e364c05f6
156 | | 1FTpAbQa4h8trvhQXjXnmNhqdiGBd1oraE | 45671926166590716193865151022383844364247891967 |
157 | | 14JHoRAdmJg3XR4RjMDh6Wed6ft6hzbQe9 | 91343852333181432387730302044767688728495783935 |
158 | | 19z6waranEf8CcP8FqNgdwUe1QRxvUNKBG | 182687704666362864775460604089535377456991567871 |
159 | | 14u4nA5sugaswb6SZgn5av2vuChdMnD9E5 | 365375409332725729550921208179070754913983135743 |
160 | | 1NBC8uXJy1GiJ6drkiZa1WuKn51ps7EPTv | 730750818665451459101842416358141509827966271487 | 02e0a8b039282faf6fe0fd769cfbc4b6b4cf8758ba68220eac420e32b91ddfa673
-> Case 134 was missing -> I added the rest of known the public keys. |
|
|
|
|
|
zielar (OP)
|
 |
September 04, 2019, 05:17:58 PM |
|
This is a continuation of the popular "32 btc puzzle" ( https://bitcointalk.org/index.php?topic=1306983.0) topic with the inclusion of the latest data updated. ............................. ............................. No. |=========PRIVATE KEY IN HEX (if it was found and known)========== |===========WALLET ADDRESS===========| ===============UPPER RANGE LIMIT================ | ===================COMPRESSED PUBLIC KEY IN HEX=================== | ==SOLVED DATE==
01 | 0000000000000000000000000000000000000000000000000000000000000001 | 1BgGZ9tcN4rm9KBzDn7KprQz87SZ26SAMH | 1 | 0279be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798 | 2015-01-15
02 | 0000000000000000000000000000000000000000000000000000000000000003 | 1CUNEBjYrCn2y1SdiUMohaKUi4wpP326Lb | 3 | 02f9308a019258c31049344f85f89d5229b531c845836f99b08601f113bce036f9 | 2015-01-15
03 | 0000000000000000000000000000000000000000000000000000000000000007 | 19ZewH8Kk1PDbSNdJ97FP4EiCjTRaZMZQA | 7 | 025cbdf0646e5db4eaa398f365f2ea7a0e3d419b7e0330e39ce92bddedcac4f9bc | 2015-01-15
04 | 0000000000000000000000000000000000000000000000000000000000000008 | 1EhqbyUMvvs7BfL8goY6qcPbD6YKfPqb7e | 15 | 022f01e5e15cca351daff3843fb70f3c2f0a1bdd05e5af888a67784ef3e10a2a01 | 2015-01-15
05 | 0000000000000000000000000000000000000000000000000000000000000015 | 1E6NuFjCi27W5zoXg8TRdcSRq84zJeBW3k | 31 | 02352bbf4a4cdd12564f93fa332ce333301d9ad40271f8107181340aef25be59d5 | 2015-01-15
06 | 0000000000000000000000000000000000000000000000000000000000000031 | 1PitScNLyp2HCygzadCh7FveTnfmpPbfp8 | 63 | 03f2dac991cc4ce4b9ea44887e5c7c0bce58c80074ab9d4dbaeb28531b7739f530 | 2015-01-15
07 | 000000000000000000000000000000000000000000000000000000000000004C | 1McVt1vMtCC7yn5b9wgX1833yCcLXzueeC | 127 | 0296516a8f65774275278d0d7420a88df0ac44bd64c7bae07c3fe397c5b3300b23 | 2015-01-15
08 | 00000000000000000000000000000000000000000000000000000000000000E0 | 1M92tSqNmQLYw33fuBvjmeadirh1ysMBxK | 255 | 0308bc89c2f919ed158885c35600844d49890905c79b357322609c45706ce6b514 | 2015-01-15
09 | 00000000000000000000000000000000000000000000000000000000000001D3 | 1CQFwcjw1dwhtkVWBttNLDtqL7ivBonGPV | 511 | 0243601d61c836387485e9514ab5c8924dd2cfd466af34ac95002727e1659d60f7 | 2015-01-15
10 | 0000000000000000000000000000000000000000000000000000000000000202 | 1LeBZP5QCwwgXRtmVUvTVrraqPUokyLHqe | 1023 | 03a7a4c30291ac1db24b4ab00c442aa832f7794b5a0959bec6e8d7fee802289dcd | 2015-01-15
11 | 0000000000000000000000000000000000000000000000000000000000000483 | 1PgQVLmst3Z314JrQn5TNiys8Hc38TcXJu | 2047 | 038b05b0603abd75b0c57489e451f811e1afe54a8715045cdf4888333f3ebc6e8b | 2015-01-15
12 | 0000000000000000000000000000000000000000000000000000000000000A7B | 1DBaumZxUkM4qMQRt2LVWyFJq5kDtSZQot | 4095 | 038b00fcbfc1a203f44bf123fc7f4c91c10a85c8eae9187f9d22242b4600ce781c | 2015-01-15
13 | 0000000000000000000000000000000000000000000000000000000000001460 | 1Pie8JkxBT6MGPz9Nvi3fsPkr2D8q3GBc1 | 8191 | 03aadaaab1db8d5d450b511789c37e7cfeb0eb8b3e61a57a34166c5edc9a4b869d | 2015-01-15
14 | 0000000000000000000000000000000000000000000000000000000000002930 | 1ErZWg5cFCe4Vw5BzgfzB74VNLaXEiEkhk | 16383 | 03b4f1de58b8b41afe9fd4e5ffbdafaeab86c5db4769c15d6e6011ae7351e54759 | 2015-01-15
15 | 00000000000000000000000000000000000000000000000000000000000068F3 | 1QCbW9HWnwQWiQqVo5exhAnmfqKRrCRsvW | 32767 | 02fea58ffcf49566f6e9e9350cf5bca2861312f422966e8db16094beb14dc3df2c | 2015-01-15
16 | 000000000000000000000000000000000000000000000000000000000000C936 | 1BDyrQ6WoF8VN3g9SAS1iKZcPzFfnDVieY | 65535 | 029d8c5d35231d75eb87fd2c5f05f65281ed9573dc41853288c62ee94eb2590b7a | 2015-01-15
17 | 000000000000000000000000000000000000000000000000000000000001764F | 1HduPEXZRdG26SUT5Yk83mLkPyjnZuJ7Bm | 131071 | 033f688bae8321b8e02b7e6c0a55c2515fb25ab97d85fda842449f7bfa04e128c3 | 2015-01-15
18 | 000000000000000000000000000000000000000000000000000000000003080D | 1GnNTmTVLZiqQfLbAdp9DVdicEnB5GoERE | 262143 | 020ce4a3291b19d2e1a7bf73ee87d30a6bdbc72b20771e7dfff40d0db755cd4af1 | 2015-01-15
19 | 000000000000000000000000000000000000000000000000000000000005749F | 1NWmZRpHH4XSPwsW6dsS3nrNWfL1yrJj4w | 524287 | 0385663c8b2f90659e1ccab201694f4f8ec24b3749cfe5030c7c3646a709408e19 | 2015-01-15
20 | 00000000000000000000000000000000000000000000000000000000000D2C55 | 1HsMJxNiV7TLxmoF6uJNkydxPFDog4NQum | 1048575 | 033c4a45cbd643ff97d77f41ea37e843648d50fd894b864b0d52febc62f6454f7c | 2015-01-15
21 | 00000000000000000000000000000000000000000000000000000000001BA534 | 14oFNXucftsHiUMY8uctg6N487riuyXs4h | 2097151 | 031a746c78f72754e0be046186df8a20cdce5c79b2eda76013c647af08d306e49e | 2015-01-15
22 | 00000000000000000000000000000000000000000000000000000000002DE40F | 1CfZWK1QTQE3eS9qn61dQjV89KDjZzfNcv | 4194303 | 023ed96b524db5ff4fe007ce730366052b7c511dc566227d929070b9ce917abb43 | 2015-01-15
23 | 0000000000000000000000000000000000000000000000000000000000556E52 | 1L2GM8eE7mJWLdo3HZS6su1832NX2txaac | 8388607 | 03f82710361b8b81bdedb16994f30c80db522450a93e8e87eeb07f7903cf28d04b | 2015-01-15
24 | 0000000000000000000000000000000000000000000000000000000000DC2A04 | 1rSnXMr63jdCuegJFuidJqWxUPV7AtUf7 | 16777215 | 036ea839d22847ee1dce3bfc5b11f6cf785b0682db58c35b63d1342eb221c3490c | 2015-01-15
25 | 0000000000000000000000000000000000000000000000000000000001FA5EE5 | 15JhYXn6Mx3oF4Y7PcTAv2wVVAuCFFQNiP | 33554431 | 03057fbea3a2623382628dde556b2a0698e32428d3cd225f3bd034dca82dd7455a | 2015-01-15
26 | 000000000000000000000000000000000000000000000000000000000340326E | 1JVnST957hGztonaWK6FougdtjxzHzRMMg | 67108863 | 024e4f50a2a3eccdb368988ae37cd4b611697b26b29696e42e06d71368b4f3840f | 2015-01-15
27 | 0000000000000000000000000000000000000000000000000000000006AC3875 | 128z5d7nN7PkCuX5qoA4Ys6pmxUYnEy86k | 134217727 | 031a864bae3922f351f1b57cfdd827c25b7e093cb9c88a72c1cd893d9f90f44ece | 2015-01-15
28 | 000000000000000000000000000000000000000000000000000000000D916CE8 | 12jbtzBb54r97TCwW3G1gCFoumpckRAPdY | 268435455 | 03e9e661838a96a65331637e2a3e948dc0756e5009e7cb5c36664d9b72dd18c0a7 | 2015-01-16
29 | 0000000000000000000000000000000000000000000000000000000017E2551E | 19EEC52krRUK1RkUAEZmQdjTyHT7Gp1TYT | 536870911 | 026caad634382d34691e3bef43ed4a124d8909a8a3362f91f1d20abaaf7e917b36 | 2015-01-16
30 | 000000000000000000000000000000000000000000000000000000003D94CD64 | 1LHtnpd8nU5VHEMkG2TMYYNUjjLc992bps | 1073741823 | 030d282cf2ff536d2c42f105d0b8588821a915dc3f9a05bd98bb23af67a2e92a5b | 2015-01-16
31 | 000000000000000000000000000000000000000000000000000000007D4FE747 | 1LhE6sCTuGae42Axu1L1ZB7L96yi9irEBE | 2147483647 | 0387dc70db1806cd9a9a76637412ec11dd998be666584849b3185f7f9313c8fd28 | 2015-01-16
32 | 00000000000000000000000000000000000000000000000000000000B862A62E | 1FRoHA9xewq7DjrZ1psWJVeTer8gHRqEvR | 4294967295 | 0209c58240e50e3ba3f833c82655e8725c037a2294e14cf5d73a5df8d56159de69 | 2015-01-16
33 | 00000000000000000000000000000000000000000000000000000001A96CA8D8 | 187swFMjz1G54ycVU56B7jZFHFTNVQFDiu | 8589934591 | 03a355aa5e2e09dd44bb46a4722e9336e9e3ee4ee4e7b7a0cf5785b283bf2ab579 | 2015-01-17
34 | 000000000000000000000000000000000000000000000000000000034A65911D | 1PWABE7oUahG2AFFQhhvViQovnCr4rEv7Q | 17179869183 | 033cdd9d6d97cbfe7c26f902faf6a435780fe652e159ec953650ec7b1004082790 | 2015-01-17
35 | 00000000000000000000000000000000000000000000000000000004AED21170 | 1PWCx5fovoEaoBowAvF5k91m2Xat9bMgwb | 34359738367 | 02f6a8148a62320e149cb15c544fe8a25ab483a0095d2280d03b8a00a7feada13d | 2015-01-17
36 | 00000000000000000000000000000000000000000000000000000009DE820A7C | 1Be2UF9NLfyLFbtm3TCbmuocc9N1Kduci1 | 68719476735 | 02b3e772216695845fa9dda419fb5daca28154d8aa59ea302f05e916635e47b9f6 | 2015-01-18
37 | 0000000000000000000000000000000000000000000000000000001757756A93 | 14iXhn8bGajVWegZHJ18vJLHhntcpL4dex | 137438953471 | 027d2c03c3ef0aec70f2c7e1e75454a5dfdd0e1adea670c1b3a4643c48ad0f1255 | 2015-01-19
38 | 00000000000000000000000000000000000000000000000000000022382FACD0 | 1HBtApAFA9B2YZw3G2YKSMCtb3dVnjuNe2 | 274877906943 | 03c060e1e3771cbeccb38e119c2414702f3f5181a89652538851d2e3886bdd70c6 | 2015-01-21
39 | 0000000000000000000000000000000000000000000000000000004B5F8303E9 | 122AJhKLEfkFBaGAd84pLp1kfE7xK3GdT8 | 549755813887 | 022d77cd1467019a6bf28f7375d0949ce30e6b5815c2758b98a74c2700bc006543 | 2015-01-30
40 | 000000000000000000000000000000000000000000000000000000E9AE4933D6 | 1EeAxcprB2PpCnr34VfZdFrkUWuxyiNEFv | 1099511627775 | 03a2efa402fd5268400c77c20e574ba86409ededee7c4020e4b9f0edbee53de0d4 | 2015-01-30
41 | 00000000000000000000000000000000000000000000000000000153869ACC5B | 1L5sU9qvJeuwQUdt4y1eiLmquFxKjtHr3E | 2199023255551 | 03b357e68437da273dcf995a474a524439faad86fc9effc300183f714b0903468b | 2015-01-30
42 | 000000000000000000000000000000000000000000000000000002A221C58D8F | 1E32GPWgDyeyQac4aJxm9HVoLrrEYPnM4N | 4398046511103 | 03eec88385be9da803a0d6579798d977a5d0c7f80917dab49cb73c9e3927142cb6 | 2015-01-30
43 | 000000000000000000000000000000000000000000000000000006BD3B27C591 | 1PiFuqGpG8yGM5v6rNHWS3TjsG6awgEGA1 | 8796093022207 | 02a631f9ba0f28511614904df80d7f97a4f43f02249c8909dac92276ccf0bcdaed | 2015-01-30 ( )
44 | 00000000000000000000000000000000000000000000000000000E02B35A358F | 1CkR2uS7LmFwc3T2jV8C1BhWb5mQaoxedF | 17592186044415 | 025e466e97ed0e7910d3d90ceb0332df48ddf67d456b9e7303b50a3d89de357336 | 2015-01-30
45 | 0000000000000000000000000000000000000000000000000000122FCA143C05 | 1NtiLNGegHWE3Mp9g2JPkgx6wUg4TW7bbk | 35184372088831 | 026ecabd2d22fdb737be21975ce9a694e108eb94f3649c586cc7461c8abf5da71a | 2015-01-30
46 | 00000000000000000000000000000000000000000000000000002EC18388D544 | 1F3JRMWudBaj48EhwcHDdpeuy2jwACNxjP | 70368744177663 | 03fd5487722d2576cb6d7081426b66a3e2986c1ce8358d479063fb5f2bb6dd5849 | 2015-09-01
47 | 00000000000000000000000000000000000000000000000000006CD610B53CBA | 1Pd8VvT49sHKsmqrQiP61RsVwmXCZ6ay7Z | 140737488355327 | 023a12bd3caf0b0f77bf4eea8e7a40dbe27932bf80b19ac72f5f5a64925a594196 | 2015-09-01
48 | 0000000000000000000000000000000000000000000000000000ADE6D7CE3B9B | 1DFYhaB2J9q1LLZJWKTnscPWos9VBqDHzv | 281474976710655 | 0291bee5cf4b14c291c650732faa166040e4c18a14731f9a930c1e87d3ec12debb | 2015-09-01
49 | 000000000000000000000000000000000000000000000000000174176B015F4D | 12CiUhYVTTH33w3SPUBqcpMoqnApAV4WCF | 562949953421311 | 02591d682c3da4a2a698633bf5751738b67c343285ebdc3492645cb44658911484 | 2015-09-01
50 | 00000000000000000000000000000000000000000000000000022BD43C2E9354 | 1MEzite4ReNuWaL5Ds17ePKt2dCxWEofwk | 1125899906842623 | 03f46f41027bbf44fafd6b059091b900dad41e6845b2241dc3254c7cdd3c5a16c6 | 2017-04-05
51 | 00000000000000000000000000000000000000000000000000075070A1A009D4 | 1NpnQyZ7x24ud82b7WiRNvPm6N8bqGQnaS | 2251799813685247 | 028c6c67bef9e9eebe6a513272e50c230f0f91ed560c37bc9b033241ff6c3be78f | 2017-04-21
52 | 000000000000000000000000000000000000000000000000000EFAE164CB9E3C | 15z9c9sVpu6fwNiK7dMAFgMYSK4GqsGZim | 4503599627370495 | 0374c33bd548ef02667d61341892134fcf216640bc2201ae61928cd0874f6314a7 | 2017-09-04
53 | 00000000000000000000000000000000000000000000000000180788E47E326C | 15K1YKJMiJ4fpesTVUcByoz334rHmknxmT | 9007199254740991 | 020faaf5f3afe58300a335874c80681cf66933e2a7aeb28387c0d28bb048bc6349 | 2017-09-04
54 | 00000000000000000000000000000000000000000000000000236FB6D5AD1F43 | 1KYUv7nSvXx4642TKeuC2SNdTk326uUpFy | 18014398509481983 | 034af4b81f8c450c2c870ce1df184aff1297e5fcd54944d98d81e1a545ffb22596 | 2017-11-16
55 | 000000000000000000000000000000000000000000000000006ABE1F9B67E114 | 1LzhS3k3e9Ub8i2W1V8xQFdB8n2MYCHPCa | 36028797018963967 | 0385a30d8413af4f8f9e6312400f2d194fe14f02e719b24c3f83bf1fd233a8f963 | 2018-05-29
56 | 000000000000000000000000000000000000000000000000009D18B63AC4FFDF | 17aPYR1m6pVAacXg1PTDDU7XafvK1dxvhi | 72057594037927935 | 033f2db2074e3217b3e5ee305301eeebb1160c4fa1e993ee280112f6348637999a | 2018-09-08
57 | 00000000000000000000000000000000000000000000000001EB25C90795D61C | 15c9mPGLku1HuW9LRtBf4jcHVpBUt8txKz | 144115188075855871 | 02a521a07e98f78b03fc1e039bc3a51408cd73119b5eb116e583fe57dc8db07aea | 2018-11-08
58 | 00000000000000000000000000000000000000000000000002C675B852189A21 | 1Dn8NF8qDyyfHMktmuoQLGyjWmZXgvosXf | 288230376151711743 | 0311569442e870326ceec0de24eb5478c19e146ecd9d15e4666440f2f638875f42 | 2018-12-03
59 | 00000000000000000000000000000000000000000000000007496CBB87CAB44F | 1HAX2n9Uruu9YDt4cqRgYcvtGvZj1rbUyt | 576460752303423487 | 0241267d2d7ee1a8e76f8d1546d0d30aefb2892d231cee0dde7776daf9f8021485 | 2019-02-11
60 | 0000000000000000000000000000000000000000000000000FC07A1825367BBE | 1Kn5h2qpgw9mWE5jKpk8PP4qvvJ1QVy8su | 1152921504606846975 | 0348e843dc5b1bd246e6309b4924b81543d02b16c8083df973a89ce2c7eb89a10d | 2019-02-17
61 | 00000000000000000000000000000000000000000000000013C96A3742F64906 | 1AVJKwzs9AskraJLGHAZPiaZcrpDr1U6AB | 2305843009213693951 | 0249a43860d115143c35c09454863d6f82a95e47c1162fb9b2ebe0186eb26f453f | 2019-05-11
62 | | 1Me6EfpwZK5kQziBwBfvLiHjaPGxCKLoJi | 4611686018427387903 |
63 | 0000000000000000000000000000000000000000000000007CCE5EFDACCF6808 | 1NpYjtLira16LfGbGwZJ5JbDPh3ai9bjf4 | 9223372036854775807 | 0365ec2994b8cc0a20d40dd69edfe55ca32a54bcbbaa6b0ddcff36049301a54579 | 2019-06-07 (zielar)
64 | | 16jY7qLJnxb7CHZyqBP8qca9d51gAjyXQN | 18446744073709551615 |
65 | 000000000000000000000000000000000000000000000001A838B13505B26867 | 18ZMbwUFLMHoZBbfpCjUJQTCMCbktshgpe | 36893488147419103231 | 0230210c23b1a047bc9bdbb13448e67deddc108946de6de639bcc75d47c0216b1b | 2019-06-07
66 | | 13zb1hQbWVsc2S7ZTZnP2G4undNNpdh5so | 73786976294838206463 |
67 | | 1BY8GQbnueYofwSuFAT3USAhGjPrkxDdW9 | 147573952589676412927 |
68 | | 1MVDYgVaSN6iKKEsbzRUAYFrYJadLYZvvZ | 295147905179352825855 |
69 | | 19vkiEajfhuZ8bs8Zu2jgmC6oqZbWqhxhG | 590295810358705651711 |
70 | 0000000000000000000000000000000000000000000000349B84B6431A6C4EF1 | 19YZECXj3SxEZMoUeJ1yiPsw8xANe7M7QR | 1180591620717411303423 | 0290e6900a58d33393bc1097b5aed31f2e4e7cbd3e5466af958665bc0121248483 | 2019-06-09
71 | | 1PWo3JeB9jrGwfHDNpdGK54CRas7fsVzXU | 2361183241434822606847 |
72 | | 1JTK7s9YVYywfm5XUH7RNhHJH1LshCaRFR | 4722366482869645213695 |
73 | | 12VVRNPi4SJqUTsp6FmqDqY5sGosDtysn4 | 9444732965739290427391 |
74 | | 1FWGcVDK3JGzCC3WtkYetULPszMaK2Jksv | 18889465931478580854783 |
75 | 0000000000000000000000000000000000000000000004C5CE114686A1336E07 | 1J36UjUByGroXcCvmj13U6uwaVv9caEeAt | 37778931862957161709567 | 03726b574f193e374686d8e12bc6e4142adeb06770e0a2856f5e4ad89f66044755 | 2019-06-10
76 | | 1DJh2eHFYQfACPmrvpyWc8MSTYKh7w9eRF | 75557863725914323419135 |
77 | | 1Bxk4CQdqL9p22JEtDfdXMsng1XacifUtE | 151115727451828646838271 |
78 | | 15qF6X51huDjqTmF9BJgxXdt1xcj46Jmhb | 302231454903657293676543 |
79 | | 1ARk8HWJMn8js8tQmGUJeQHjSE7KRkn2t8 | 604462909807314587353087 |
80 | 00000000000000000000000000000000000000000000EA1A5C66DCC11B5AD180 | 1BCf6rHUW6m3iH2ptsvnjgLruAiPQQepLe | 1208925819614629174706175 | 037e1238f7b1ce757df94faa9a2eb261bf0aeb9f84dbf81212104e78931c2a19dc | 2019-06-11
81 | | 15qsCm78whspNQFydGJQk5rexzxTQopnHZ | 2417851639229258349412351 |
82 | | 13zYrYhhJxp6Ui1VV7pqa5WDhNWM45ARAC | 4835703278458516698824703 |
83 | | 14MdEb4eFcT3MVG5sPFG4jGLuHJSnt1Dk2 | 9671406556917033397649407 |
84 | | 1CMq3SvFcVEcpLMuuH8PUcNiqsK1oicG2D | 19342813113834066795298815 |
85 | 00000000000000000000000000000000000000000011720C4F018D51B8CEBBA8 | 1Kh22PvXERd2xpTQk3ur6pPEqFeckCJfAr | 38685626227668133590597631 | 0329c4574a4fd8c810b7e42a4b398882b381bcd85e40c6883712912d167c83e73a | 2019-06-17
86 | | 1K3x5L6G57Y494fDqBfrojD28UJv4s5JcK | 77371252455336267181195263 |
87 | | 1PxH3K1Shdjb7gSEoTX7UPDZ6SH4qGPrvq | 154742504910672534362390527 |
88 | | 16AbnZjZZipwHMkYKBSfswGWKDmXHjEpSf | 309485009821345068724781055 |
89 | | 19QciEHbGVNY4hrhfKXmcBBCrJSBZ6TaVt | 618970019642690137449562111 |
90 | 000000000000000000000000000000000000000002CE00BB2136A445C71E85BF | 1L12FHH2FHjvTviyanuiFVfmzCy46RRATU | 1237940039285380274899124223 | 035c38bd9ae4b10e8a250857006f3cfd98ab15a6196d9f4dfd25bc7ecc77d788d5 | 2019-07-01
91 | | 1EzVHtmbN4fs4MiNk3ppEnKKhsmXYJ4s74 | 2475880078570760549798248447 |
92 | | 1AE8NzzgKE7Yhz7BWtAcAAxiFMbPo82NB5 | 4951760157141521099596496895 |
93 | | 17Q7tuG2JwFFU9rXVj3uZqRtioH3mx2Jad | 9903520314283042199192993791 |
94 | | 1K6xGMUbs6ZTXBnhw1pippqwK6wjBWtNpL | 19807040628566084398385987583 |
95 | 0000000000000000000000000000000000000000527a792b183c7f64a0e8b1f4 | 19eVSDuizydXxhohGh8Ki9WY9KsHdSwoQC | 39614081257132168796771975167 | 02967a5905d6f3b420959a02789f96ab4c3223a2c4d2762f817b7895c5bc88a045 | 2019-07-06
96 | | 15ANYzzCp5BFHcCnVFzXqyibpzgPLWaD8b | 79228162514264337593543950335 |
97 | | 18ywPwj39nGjqBrQJSzZVq2izR12MDpDr8 | 158456325028528675187087900671 |
98 | | 1CaBVPrwUxbQYYswu32w7Mj4HR4maNoJSX | 316912650057057350374175801343 |
99 | | 1JWnE6p6UN7ZJBN7TtcbNDoRcjFtuDWoNL | 633825300114114700748351602687 |
100 | 000000000000000000000000000000000000000af55fc59c335c8ec67ed24826 | 1KCgMv8fo2TPBpddVi9jqmMmcne9uSNJ5F | 1267650600228229401496703205375 | 03d2063d40402f030d4cc71331468827aa41a8a09bd6fd801ba77fb64f8e67e617 | 2019-07-08
101 | | 1CKCVdbDJasYmhswB6HKZHEAnNaDpK7W4n | 2535301200456458802993406410751 |
102 | | 1PXv28YxmYMaB8zxrKeZBW8dt2HK7RkRPX | 5070602400912917605986812821503 |
103 | | 1AcAmB6jmtU6AiEcXkmiNE9TNVPsj9DULf | 10141204801825835211973625643007 |
104 | | 1EQJvpsmhazYCcKX5Au6AZmZKRnzarMVZu | 20282409603651670423947251286015 |
105 | | 1CMjscKB3QW7SDyQ4c3C3DEUHiHRhiZVib | 40564819207303340847894502572031 | 03bcf7ce887ffca5e62c9cabbdb7ffa71dc183c52c04ff4ee5ee82e0c55c39d77b
106 | | 18KsfuHuzQaBTNLASyj15hy4LuqPUo1FNB | 81129638414606681695789005144063 |
107 | | 15EJFC5ZTs9nhsdvSUeBXjLAuYq3SWaxTc | 162259276829213363391578010288127 |
108 | | 1HB1iKUqeffnVsvQsbpC6dNi1XKbyNuqao | 324518553658426726783156020576255 |
109 | | 1GvgAXVCbA8FBjXfWiAms4ytFeJcKsoyhL | 649037107316853453566312041152511 |
110 | | 12JzYkkN76xkwvcPT6AWKZtGX6w2LAgsJg | 1298074214633706907132624082305023 | 0309976ba5570966bf889196b7fdf5a0f9a1e9ab340556ec29f8bb60599616167d
111 | | 1824ZJQ7nKJ9QFTRBqn7z7dHV5EGpzUpH3 | 2596148429267413814265248164610047 |
112 | | 18A7NA9FTsnJxWgkoFfPAFbQzuQxpRtCos | 5192296858534827628530496329220095 |
113 | | 1NeGn21dUDDeqFQ63xb2SpgUuXuBLA4WT4 | 10384593717069655257060992658440191 |
114 | | 174SNxfqpdMGYy5YQcfLbSTK3MRNZEePoy | 20769187434139310514121985316880383 |
115 | | 1NLbHuJebVwUZ1XqDjsAyfTRUPwDQbemfv | 41538374868278621028243970633760767 | 0248d313b0398d4923cdca73b8cfa6532b91b96703902fc8b32fd438a3b7cd7f55
116 | | 1MnJ6hdhvK37VLmqcdEwqC3iFxyWH2PHUV | 83076749736557242056487941267521535 |
117 | | 1KNRfGWw7Q9Rmwsc6NT5zsdvEb9M2Wkj5Z | 166153499473114484112975882535043071 |
118 | | 1PJZPzvGX19a7twf5HyD2VvNiPdHLzm9F6 | 332306998946228968225951765070086143 |
119 | | 1GuBBhf61rnvRe4K8zu8vdQB3kHzwFqSy7 | 664613997892457936451903530140172287 |
120 | | 17s2b9ksz5y7abUm92cHwG8jEPCzK3dLnT | 1329227995784915872903807060280344575 | 02ceb6cbbcdbdf5ef7150682150f4ce2c6f4807b349827dcdbdd1f2efa885a2630
121 | | 1GDSuiThEV64c166LUFC9uDcVdGjqkxKyh | 2658455991569831745807614120560689151 |
122 | | 1Me3ASYt5JCTAK2XaC32RMeH34PdprrfDx | 5316911983139663491615228241121378303 |
123 | | 1CdufMQL892A69KXgv6UNBD17ywWqYpKut | 10633823966279326983230456482242756607 |
124 | | 1BkkGsX9ZM6iwL3zbqs7HWBV7SvosR6m8N | 21267647932558653966460912964485513215 |
125 | | 1PXAyUB8ZoH3WD8n5zoAthYjN15yN5CVq5 | 42535295865117307932921825928971026431 | 0233709eb11e0d4439a729f21c2c443dedb727528229713f0065721ba8fa46f00e
126 | | 1AWCLZAjKbV1P7AHvaPNCKiB7ZWVDMxFiz | 85070591730234615865843651857942052863 |
127 | | 1G6EFyBRU86sThN3SSt3GrHu1sA7w7nzi4 | 170141183460469231731687303715884105727 |
128 | | 1MZ2L1gFrCtkkn6DnTT2e4PFUTHw9gNwaj | 340282366920938463463374607431768211455 |
129 | | 1Hz3uv3nNZzBVMXLGadCucgjiCs5W9vaGz | 680564733841876926926749214863536422911 |
130 | | 1Fo65aKq8s8iquMt6weF1rku1moWVEd5Ua | 1361129467683753853853498429727072845823 | 03633cbe3ec02b9401c5effa144c5b4d22f87940259634858fc7e59b1c09937852
131 | | 16zRPnT8znwq42q7XeMkZUhb1bKqgRogyy | 2722258935367507707706996859454145691647 |
132 | | 1KrU4dHE5WrW8rhWDsTRjR21r8t3dsrS3R | 5444517870735015415413993718908291383295 |
133 | | 17uDfp5r4n441xkgLFmhNoSW1KWp6xVLD | 10889035741470030830827987437816582766591 |
134 | | 13A3JrvXmvg5w9XGvyyR4JEJqiLz8ZySY3 | 16333553612205046246241981156724874149887 |
135 | | 16RGFo6hjq9ym6Pj7N5H7L1NR1rVPJyw2v | 21778071482940061661655974875633165533183 | 02145d2611c823a396ef6712ce0f712f09b9b4f3135e3e0aa3230fb9b6d08d1e16
136 | | 1UDHPdovvR985NrWSkdWQDEQ1xuRiTALq | 43556142965880123323311949751266331066367 |
137 | | 15nf31J46iLuK1ZkTnqHo7WgN5cARFK3RA | 87112285931760246646623899502532662132735 |
138 | | 1Ab4vzG6wEQBDNQM1B2bvUz4fqXXdFk2WT | 174224571863520493293247799005065324265471 |
139 | | 1Fz63c775VV9fNyj25d9Xfw3YHE6sKCxbt | 348449143727040986586495598010130648530943 |
140 | | 1QKBaU6WAeycb3DbKbLBkX7vJiaS8r42Xo | 696898287454081973172991196020261297061887 | 031f6a332d3c5c4f2de2378c012f429cd109ba07d69690c6c701b6bb87860d6640
141 | | 1CD91Vm97mLQvXhrnoMChhJx4TP9MaQkJo | 1393796574908163946345982392040522594123775 |
142 | | 15MnK2jXPqTMURX4xC3h4mAZxyCcaWWEDD | 2787593149816327892691964784081045188247551 |
143 | | 13N66gCzWWHEZBxhVxG18P8wyjEWF9Yoi1 | 5575186299632655785383929568162090376495103 |
144 | | 1NevxKDYuDcCh1ZMMi6ftmWwGrZKC6j7Ux | 11150372599265311570767859136324180752990207 |
145 | | 19GpszRNUej5yYqxXoLnbZWKew3KdVLkXg | 22300745198530623141535718272648361505980415 | 03afdda497369e219a2c1c369954a930e4d3740968e5e4352475bcffce3140dae5
146 | | 1M7ipcdYHey2Y5RZM34MBbpugghmjaV89P | 44601490397061246283071436545296723011960831 |
147 | | 18aNhurEAJsw6BAgtANpexk5ob1aGTwSeL | 89202980794122492566142873090593446023921663 |
148 | | 1FwZXt6EpRT7Fkndzv6K4b4DFoT4trbMrV | 178405961588244985132285746181186892047843327 |
149 | | 1CXvTzR6qv8wJ7eprzUKeWxyGcHwDYP1i2 | 356811923176489970264571492362373784095686655 |
150 | | 1MUJSJYtGPVGkBCTqGspnxyHahpt5Te8jy | 713623846352979940529142984724747568191373311 | 03137807790ea7dc6e97901c2bc87411f45ed74a5629315c4e4b03a0a102250c49
151 | | 13Q84TNNvgcL3HJiqQPvyBb9m4hxjS3jkV | 1427247692705959881058285969449495136382746623 |
152 | | 1LuUHyrQr8PKSvbcY1v1PiuGuqFjWpDumN | 2854495385411919762116571938898990272765493247 |
153 | | 18192XpzzdDi2K11QVHR7td2HcPS6Qs5vg | 5708990770823839524233143877797980545530986495 |
154 | | 1NgVmsCCJaKLzGyKLFJfVequnFW9ZvnMLN | 11417981541647679048466287755595961091061972991 |
155 | | 1AoeP37TmHdFh8uN72fu9AqgtLrUwcv2wJ | 22835963083295358096932575511191922182123945983 | 035cd1854cae45391ca4ec428cc7e6c7d9984424b954209a8eea197b9e364c05f6
156 | | 1FTpAbQa4h8trvhQXjXnmNhqdiGBd1oraE | 45671926166590716193865151022383844364247891967 |
157 | | 14JHoRAdmJg3XR4RjMDh6Wed6ft6hzbQe9 | 91343852333181432387730302044767688728495783935 |
158 | | 19z6waranEf8CcP8FqNgdwUe1QRxvUNKBG | 182687704666362864775460604089535377456991567871 |
159 | | 14u4nA5sugaswb6SZgn5av2vuChdMnD9E5 | 365375409332725729550921208179070754913983135743 |
160 | | 1NBC8uXJy1GiJ6drkiZa1WuKn51ps7EPTv | 730750818665451459101842416358141509827966271487 | 02e0a8b039282faf6fe0fd769cfbc4b6b4cf8758ba68220eac420e32b91ddfa673
-> Case 134 was missing -> I added the rest of known the public keys. Thank you. i would like to edit table when i back to home, but all known public keys is already aż added to table from ~2 weeks |
If you want - you can send me a donation to my BTC wallet address 31hgbukdkehcuxcedchkdbsrygegyefbvd
|
|
|
racminer
Member
 
 Offline Offline
Activity: 242
Merit: 17

|
 |
September 05, 2019, 07:26:14 AM |
|
Kangaroo System, test friends.
Can you share your scan time and speed?
and How many bits?
I'm
48 bit - 110k / s - 87 sec
51 bit - 110k / s - 200 sec
60 bit - 100k/s - 3900 sec |
|
|
|
|
brainless
Member
 
 Offline Offline
Activity: 318
Merit: 34

|
 |
September 05, 2019, 09:46:20 AM |
|
Kangaroo System, test friends.
Can you share your scan time and speed?
and How many bits?
I'm
48 bit - 110k / s - 87 sec
51 bit - 110k / s - 200 sec
60 bit - 100k/s - 3900 sec can your share modified script for search range... ? PM me |
13sXkWqtivcMtNGQpskD78iqsgVy9hcHLF
|
|
|
racminer
Member
 
 Offline Offline
Activity: 242
Merit: 17

|
 |
September 05, 2019, 12:45:11 PM |
|
Kangaroo System, test friends.
Can you share your scan time and speed?
and How many bits?
I'm
48 bit - 110k / s - 87 sec
51 bit - 110k / s - 200 sec
60 bit - 100k/s - 3900 sec can your share modified script for search range... ? PM me I did nothing fancy, just followed this http://fe57.org/forum/thread.php?board=4&thema=1#1in particular:
20.08.19 19:37 Administrator
57feRe: Pollard's kangaroo with Python 2.7
niidt:
At what point does your code start searching?
With the first key 00000000000000000000000000000000000000000000000000000000000000000000000000000001?
And for example, you can not specify a range?
Search range is defined in line 125 of the code by tamed kangaroos placement. Tamed herd placed randomly from (a+b)/2 to (a+b)/2+(b-a),
where (a,b) is 'a priory' range for private key to solve. Such selection provides best overlapping of tame and wild herds.
Kangaroo from wild herd has only relative displacement from known EC-point P (line 129). Therefore their offset from P varies from 0 to (b-a)
in the Puzzle.
|
|
|
|
|
racminer
Member
 
 Offline Offline
Activity: 242
Merit: 17

|
 |
September 05, 2019, 10:26:50 PM
Last edit: September 05, 2019, 11:12:16 PM by racminer |
|
He is an example that shows that 57feRe code works well. Nice tool for fast recovery of partial private key loss when public key is known using one core CPU.
PUBKEY 03B5406C79568685D9ECFC547DFF8CD373A6417ED259007215AAF52442C808EA7A
PVKRANGE 6972ACF5B21F4C39E5E521CEAAB9506FADEDBD65C766B8DDAFA2B00000000000 6972ACF5B21F4C39E5E521CEAAB9506FADEDBD65C766B8DDAFA2C00000000000
P-table prepared
tame and wild herds are prepared
165167.102 h/s
165239.354 h/s
165142.364 h/s
164965.314 h/s
164286.715 h/s
164979.066 h/s
total time: 33.44 sec
SOLVED: 6972acf5b21f4c39e5e521ceaab9506fadedbd65c766b8ddafa2bc631fe53f81
('Hops:', 5510227)
With Bitcrack and a 100Mkey/s gpu , you need 4096 secondes.
|
|
|
|
|
racminer
Member
 
 Offline Offline
Activity: 242
Merit: 17

|
 |
September 06, 2019, 12:02:06 AM |
|
Another example
PUBLIC KEY 023157A9DDBEB3FBE80500BDB1C236AFF231544948DFC7C67BA4801D1CA05DECA4
PRIVATE KEY RANGE
B577461C865C17619B0EE83673E7DB4C7FFFD4A5545B8C58B100000000000000
B577461C865C17619B0EE83673E7DB4C7FFFD4A5545B8C58B200000000000000
total time: 646.40 sec
SOLVED: B577461C865C17619B0EE83673E7DB4C7FFFD4A5545B8C58B102318A916E6C98
this range counts some 72057594037927936 keys, with bitcrack and a 100MKey/s GPU , you need 22 years to scan the whole range.
|
|
|
|
|
|



