Options on bitcoin have been accessible only to whales and on very specific exchanges as Deribit, but when Bakkt and CME, the two main traditional bitcoin exchanges will open the products to their clients option trading in bitcoin will become more widely accessible.
Actually, options trading has been available on Bakkt since December 9th, while CME will launch a similar product later this month, starting trading from January 13th.
Options are a difficult instrument to trade. This is true in traditional markets, but this is even more true in a wild market like bitcoin.
With this thread, I will try to give a few theoretical and practical hints on how to understand, price and use options.
I will start detailing what an option is, explaining all the characteristics of the options and what they mean for the investor.
Then I will briefly explain how to price them. I won’t explain the details of the mathematical model used to price those, because it would imply some advanced differential calculus nobody wants to hear about. What I will try to do is to convey what factors have an impact on option price and how to interpret those. I will also try to clear the field from some common misconceptions about options.
Last I will explain a few common strategies for options trading. Nothing too complicated, just a few examples on how to use them according to investment purpose: be it speculation or hedging.
INDEX
What is an optionAn option is a contract that gives the holder the faculty, but not the obligation, to trade an asset, called the underlying asset, before the expiry, the termination date of such contract.
The option that gives the holder the
faculty to buy the underlying asset is called
call option.
The option that gives the holder the
faculty to sell the underlying asset is is called a
put option.
The price at the trade will happen is called the strike price.
When an option generates a trade then we say it is "exercised", otherwise it simply ends without any trade put in place we say it is "abandoned".
If an option can be exercised only at the termination is called European Option, while if it can be exercised anytime before the termination is called American Option.
The price the buyer of the option pays to the seller, or the writer of the option, is called the premium.
If the market price is above the strike price, the call option is called "in-the-money", because in the case of American exercise it could be exercised with profit. Otherwise, the call option is called "out-of the-money".
If the market price is below the strike of the put option, the put option is called "in-the-money", because in the case of American exercise it could be exercised with profit. Otherwise, the put option is called "out-of-the-money".
If we look at a certain strike then, only call options or put option can be in-the-money, not both of them. For example, if we look at 10,000 strike options, the calls are now out-of-the-money, while puts are in-the-money.
At expiry, if the option can generate the underlying asset what has been priced is called “physical delivery”. Many commodity or financial options are physically settled. Alternatively, an option can regulate only the cash equivalent of the profit exercising the option itself: that expiry then an in-the-money option would deliver the buyer a cash amount equal to the difference between the asset price and the strike (in case of a call option) or the difference between the strike price and the asset (in case of a put option). In this case, the option is called cash-settled.
In the case of Bitcoin options, namely the Bakkt options on BTC futures, the option is physically settled: at the expiry of the option the in-the-money option generates an appropriate position in the underlying future. There’s only a peculiarity: as it is common on many commodity options, the option itself expires a few days before the future, so the holder of the in-the-money options has the possibility to close the future position before the actual delivery of the underlying of the future (the option has the future as underlying, the future has the bitcoin as underlying). This is why you probably heard some marketing nonsense where “Bakkt options allow you to choose the type of delivery: physical or cash)".
Before analysing mathematically how to price an option, let’s see that impact the pricing with the intuition.
STRIKE: The first element is the strike. Of course, the difference between the market price and the strike is the first hint at the value of an option. Intuitively the more an option is in-the-money, then the more such an option must have value.
When an option is in-the-money, such an option has intrinsic value. For both call and put options, the intrinsic value is equal to the difference between the underlying price and the strike price: intrinsic value only measures the profit as determined by the difference between the option's strike price and market price.
When an option is out-of-the money instead, the intrinsic value is zero.
The intrinsic value is the minimum value of an option: if the value of an option would be less than the intrinsic value, could be arbitraged, buying that option and exercising it to profit.
So when BTC is trading at 7,000, a call with strike K = 5,000 is in-the-money and has an intrinsic value of 2,000, so the price must be greater than that. At the same time, a call with a strike K =10,000 has no intrinsic value, so the intrinsic value is zero.
Of course, intrinsic value is only a part of the pricing of an option: other variables impact the option pricing each one of them adding value to the intrinsic value getting the final value of the options:
TIME TO EXPIRY: the second most important element when pricing an option is the time to expiry: the longer the time to expiry, the dearer the option. If we price two options with all characteristics being equal, but the exercise date, the one with the exercise date the furthest away, will have the greater price.
VOLATILITY: the greater the volatility of the underlying asset, the greater the value of the option. Here the explanation gets a little bit tricky. Let’s say that the main reason it is not the greater the volatility of the underlying, the greater the possibility of the underlying going in-the-money. We will see later why this is important, just take in mind that is not obvious. The option buyer doesn’t profit from the option going in-the-money. Rather don’t profit only if the option goes in-the-money. The buyer of the option benefits just because the underlying asset moves (i.e. it is volatile) under a risk-neutral approach, i.e. without taking the “risk” of profiting because the option goes in-the-money.
Let's see an example:
We buy a call option on BTCUSD, with a strike price of 8,000 USD, expiring in June 2020.
The strategy is named Long call because buying something is called being "
long" in finance jargon.
The premium for this option is 1,350 USD, we have to pay immediately ("
upfront", again in finance jargon).
Fast forward to option expiry.
The outcomes of our option differ according to the final price of bitcoin:
If BTCUSD is below 8,000 USD the option is abandoned, it expires worthless.
If BTCUSD is above 8,000 USD the option is exercised, and generate a payoff equal to the difference (positive) between BTCUSD and the strike price.
In more formal terms the call option payoff is the following:
Call=max(0;Spot-Strike)
The final payoff of the strategy will be the following:
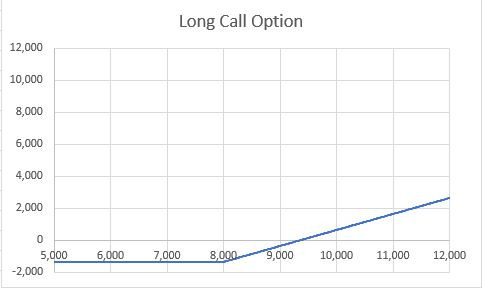
Note that this graph considers we paid a premium of 1,350 USD upfront, the premium must be paid in every scenario: if the option expires worthless the P&L (Profit&Loss) of the strategy is negative and equal to the premium paid, otherwise is equal to the option payoff netted with the premium paid.
Note that the P&L starts increasing at the strike price level, 8,000 USD in this case, but breaks even at a higher level equal to the strike + the premium plaid, or 9,350 USD in this example.
Let's see the same thing for a put option.
We buy a put option on BTCUSD, with a strike price of 6,000 USD, expiring in June 2020.
The strategy is named
long put.
The premium for this option is 732 USD, we have to pay "
upfront".
Fast forward to option expiry.
The outcomes of our option differ according to the final price of bitcoin:
If BTCUSD is above 6,000 USD the option is abandoned, it expires worthless.
If BTCUSD is below 6,000 USD the option is exercised, and generate a payoff equal to the difference (positive) between the strike price and the BTCUSD.
In more formal terms the put option payoff is the following:
Put=max(0;Strike-Spot)
The final payoff of the strategy will be the following:
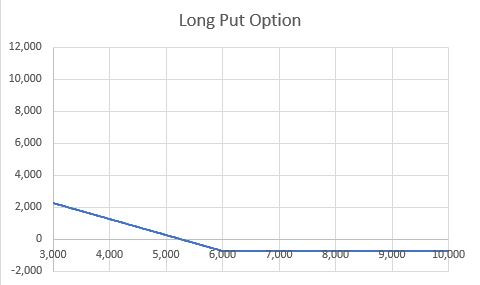
The graph looks familiar, as it is the symmetrical payoff than the call.
Note that this graph considers we paid a premium of 732 USD upfront, the premium must be paid in every scenario: if the option expires worthless the P&L of the strategy is negative and equal to the premium paid, otherwise is equal to the option payoff netted with the premium paid.
Note that the P&L starts increasing at the strike price level, 6,000 USD in this case, but breaks even at a lower-level equal to the strike - the premium plaid, or 5,267 USD in this example.
Let’s have a look at an options exchange looking for confirmations.
All the examples are from Deribit, who is the only widely available source for option prices: creating an account is easy and don’t require KYC. If you are interested to do it for educational purposes. Of course standard disclaimers apply and I am not by any mean linked to that exchange.
If we select BTC options, and then 26 Jun 2020 we will find a screen like the following:
 (click on the image to enlarge it)
(click on the image to enlarge it)This particular page considers the options maturing on 26 Jun 2020.
The centre grey column represents the strike levels. The options on the same row share the same strike price.
On the left of that column, we have the call options for each strike, while the puts are on the right-hand side.
The bid price is the price where other participants want to buy the options, i.e. the price you have to sell at if you want to sell it.
The ask price is the price where other participants want to sell the options, i.e. the price you have to pay for if you want to buy it.
Each bid and ask price has a corresponding Implied Volatility level, that is the volatility level that, if inputted in the model, gives back the aforementioned price.
This is why speaking of options, volatility and price are exchangeable concepts.
As we saw earlier, we see that the calls have a diminishing price when the strike goes up: the 6,000 call has a mid-price (the average between the bid and the ask) of 0.29725 BTC, while the 10,000 call has a mid-price of 0.11275 BTC.
The opposite is true for the puts. The puts with lower strike have lower premiums.
The put stuck at 10,000 has a price of 0.46075 BTC, while the 6,000 put has a mid-price of 0.09725 BTC.
Also, we can see that examining options with greater time to expiry each option has a greater value: the 10,000 USD strike call maturing in September has a value of 0.16775 BTC versus the value of 0.11275 of the same option maturing in June. The 6,000 strike put has a value of 0.13175 BTC versus the value of 0.09725 of the same option maturing in June.
If we plug the data we find on that page in an options calculator we can reprice the option itself.
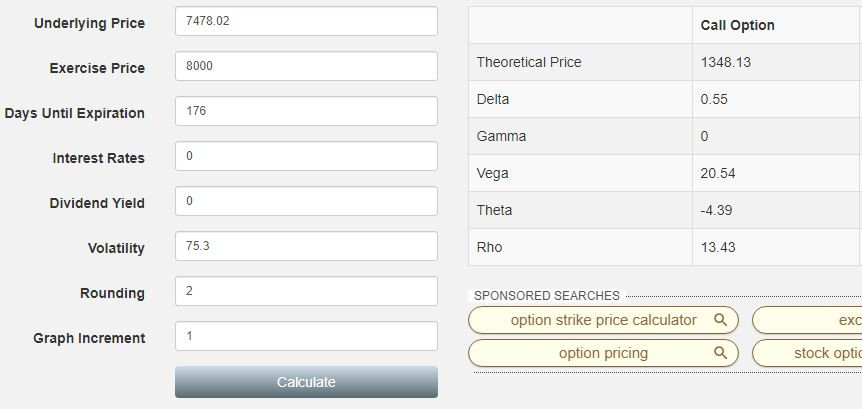
If we try to reprice the 8,000 USD call, inputting 0% as the interest rate (BTC is a non-dividend paying asset) and the correct information about strike, underlying and implied volatility, we get the (almost) exact valuation we have on Deribit:
The numbers below the option price are the
"greeks" or the sensitivities of the option price to their various component:
DELTA: it's the sensitivity of the option price to the underlying: if the underlying goes up 1 USD, the option price goes up 0.55 USD.
GAMMA: it's the second-order sensitivity of the option price to the underlying: if the underlying goes up 1 USD, the option delta goes up 0% (I guess there's a rounding factor here to consider in this calculator)
VEGA: it's the sensitivity of the option price to the volatility level: if the volatility goes up 1%, the option price goes up 20.54 USD.
THETA: it's the sensitivity of the option price to the time: if 1 day passes, the option price goes down 4.39 USD.
RHO: it's the sensitivity of the option price to the interest rates: if interest rates go to 1%, the option price goes up 13.49 USD.
The greeks of an option are linked to each other in a pretty complicated way, there are many ways to interpret them and they all varies continuously given the level of the market, the volatility and the time to maturity.
Books have been written on how to tame them and use them in your favour. I think this very brief explanation is enough for this thread.
How to price an optionUnderstanding the details of how options are priced, would mean understanding very advanced mathematics, including stochastic calculus, differential calculus, statistics, etc.
Here I want only to give you a few important concepts, you have to keep in mind when thinking of options and their value.
Black&Scholes won the Nobel prize for their option pricing model. Their biggest achievement was to demonstrate it is possible to price an option using non-arbitrage conditions. Arbitrage is a trade where a profit is gained involving no risk and no capital. Of course, those trades do not exist, so markets will adapt themselves to avoid these situations. Reasoning under the “non-arbitrage” conditions, means also that no risks are involved, hence the individual appetite for risk of each different trader in the market can be taken out of the equation. This means that every trader in the market will reason using the same “language” of a world without risk (if we reason with no-arbitrage conditions, we can ignore the associated risk, then we can ignore the willingness of every trader to take that risk). This means the price of such a derivative is unique, irrespective of the risk appetite for each trader. This has the important consequence the price of an option is INDEPENDENT of the probability given by each trader about the possibility of the underlying ending in-the-money. This is something we have to keep in mind: the price of an option doesn’t mean automatically that the scenario where it ends in-the-money is more “plausible”.
Historical Volatility vs Implied Volatility As we can see the only “difficult” input to price an option is the volatility to be used.
The correct number to be plugged into the pricer is the expected future realised volatility until the expiration of the option. Quoting this number means quoting the price of the option (being the other option pricing numbers deterministic, i.e. known without uncertainty).
The volatility level used to price an option is called implied volatility because it’s the level of volatility “implied” by the quoted price.
How do you quote the future volatility?
Here’s the trick of options trading.
The first idea is to look at the realised volatility: looking at the past can give first guidance of the future volatility. Of course, this is not always true as there can be many factors that can change the volatility in the future. One easy example, specific to bitcoin options could be the halving. This event, according to many models, could have a great impact on the bitcoin price. So we can guess that coming into the halving the volatility will be low: bitcoin might move, but without great variations, but once the halving happens, the price will possibly start swinging more, due to the very different valuation the S2F model implies. In this case realised volatility won’t be good guidance for the future volatility: namely the realised volatility will be much lower than the future volatility used to price options with expiries after the halving.
Many websites calculate the realised volatility of bitcoin: on Deribit you can get one.
Calculating historical volatility with different horizons yield very different results:

In the above graph, we see the bitcoin price (black line, left axis), with the superimposition of different historical volatility calculations using different terms (yellow, red and blue lines, right axis). Volatility in the short term can be more “volatile” itself (yes, there is the volatility of volatility, but this is for advanced options trading). The yellow line represents the annualised historical volatility calculated using the previous 10 trading days, and as we see in the above graph is swinging more violently, from 180% to below 20%. Volatility calculated over more extended periods of time, like the blue line (calculated over the last 30 days of data) or the red line (calculated over the last 180 days of data) is instead more and more stable as we extend the calculation interval.
Of course, we are more interested in matching, with the caveat earlier explained, the historical volatility computation with the time to expiry of the option we want to price.
The implied volatility can instead be observed on options markets. If we look at the options screen above we see some IV columns: that is the implied volatility corresponding to each quote. If we use the model in the opposite way, we can use the price as an input and find the volatility implied into that price: that is the implied volatility.
Option strategies - How to use an optionOptions are very complicated instruments, here I want to highlight only a few uses of them.
These are the most simple ones, and all have in common to be “static” strategies. This means those are meant to be put in place and not touched until maturity. There are different strategies meant to be adjusted during the life of the option. These are totally different animals and they are called dynamic strategies.
Leverage TradingScenario:
You want to gain as much possible exposure to bitcoin.
You have a very clear trading view.
You are not interested in losing your capital if this view doesn’t materialise.
Strategy:
Use your funding to pay the premium for an out-of-the-money option, choosing the strike to maximise the expected final payout.
Example:
- Buy 1 call option strike 7,000 USD, Jun Expiry at 0.233 BTC.
alternatively
- Buy 1 call option strike 8,000 USD, Jun Expiry for a total of 0.1805 BTC.
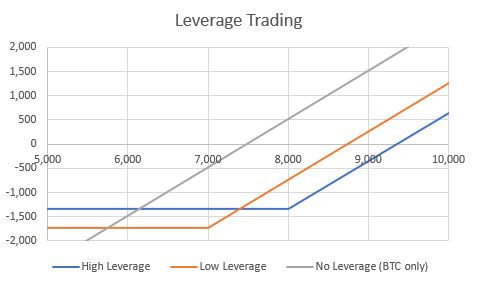
Analysis:
In this scenario, you have gained exposure to the appreciation of bitcoin above the strike level using only a fraction of the capital required to buy the underlying (i.e. 1 bitcoin).
In the case of bitcoin being at a price of 10,000 at expiry, in the case of a bitcoin investment, you would have a return equal to (10,000-8,000)/8,000=25%.
This is the base case scenario of no leverage.
Buying an in-the-money call option the return would be instead (10,000-7,000-1,742)/1,742=72%.
Note that if the option gets further in-the-money the return goes up even further as the option paid is constant, while the gain increase linearly.
In the second example, we bought an out-of-the-money option, using even less capital.
In the case of bitcoin being at a price of 10,000 at expiry, the yield would be in this case (10,000-8,000-1,350)/1,350=48%.
Of course in the scenario of an opposite movement, your loss is limited to the premium paid, which would be lost entirely.
This implies that you have to choose wisely not only the strike level, to gain the correct level of exposure, but also the expiry, as the movement has to materialise Before the expiry of the option.
Covered call writingScenario:
You are a whale you want to sell part of your bitcoin holding to finance your daily expenses. You are bullish on bitcoin as an investment.
Strategy:
Sell out-of-the-money calls, cash in the premium to finance your expenses, actually sell bitcoin only if the price goes up (possibly on a spike).
Example:
- long 1 bitcoin,
- sell 1 option strike 10,000 USD, Jun Expiry at 0.11 bitcoin.
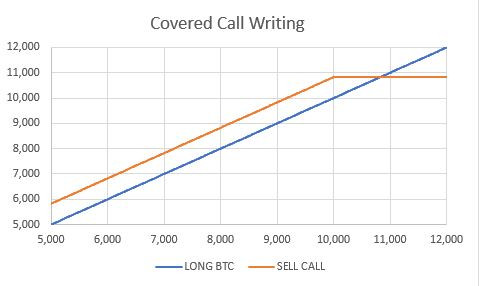
Analysis:
The payoff of the structure gives you a benefit over the simple holding of bitcoin equal to the premium if the price is below the strike price at maturity.
If at expiry the price is above the strike, the option goes in-the-money and you sell the bitcoin.
The strategy has a break-even, compared to being long the BTC only, at a level equal to strike + premium received (in this example at 10,000+0.11*7,478=10,826 roughly).
If the BTC goes further up, you basically sold a bitcoin at 10,826, hence the strategy has a lower value against holding the bitcoin.
CollarScenario:
You are a whale.
You want to sell part of your bitcoin holding to finance your daily expenses.
You are bullish on bitcoin as an investment.
You get pissed off in case of a violent drawdown in bitcoin prices.
Strategy:
Sell out-of-the-money calls, cash in the premium to finance your expenses, actually sell bitcoin only if the price goes up (possibly on a spike).
Use the cashed-in premium to buy protection on the downside, i.e. buying a put option.
Buying an out-of-the-money call and selling an out-of-the-money put is a strategy known as "Collar".
Example:
- long 1 bitcoin,
- sell 1 call option, strike 10,000 USD, Jun Expiry at 0.11 BTC,
- buy 1 put option, strike 6,000 USD, Jun Expiry for 0.098 BTC.
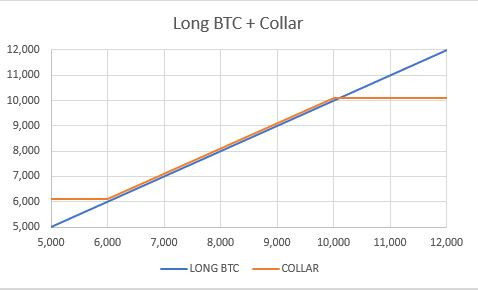
Analysis:
The final payoff is similar to the one of the covered call writing.
The payoff of the structure gives you a benefit over the simple holding of bitcoin equal to the difference between the premiums paid to buy the put and the premium cashed in to sell the call. In this particular case, I chose two strike levels to have the smallest positive difference between the twos. If the price is below the strike price at maturity.
If at expiry the price is above the strike, the option goes in-the-money and you sell the bitcoin.
The strategy has a break-even, compared to being long underlying, at a level equal to strike+premium received (in this example at 10,000+(0.11-0.098)*7478=10,093 roughly).
If the BTC goes further up, you basically sold a bitcoin at 10,093.
On the contrary, if BTC goes down, you also bought protection at 6,000, as you are long a 6,000 put. More precisely, as you cashed in a premium of 93 dollars, you are protected at a 6,093 USD. In case bitcoin goes down more, you are not affected, as the payoff of the put protects you on the downside.
Word of caution.
Options are a very complicated topic.
I tried my best effort to explain this topic in the most simple and intuitive way.
I can expand the thread in the direction you prefer. Just ask me to explain what you are interested in most, or just ask me to clarify the point you want me to dig more precisely.
If you think this thread or
any other of my threads is worth being translated in your own local board, please do! I will be happy to provide assistance!
Useful resources:
Online Calculators:
Option CalculatorExchanges product information:
Option on Bakkt ™ Bitcoin (USD) Monthly FuturesOptions on Bitcoin FuturesOnline courses:
Basic:
CME Option CourseAdvanced:
Options Theory for Professional Trading
This post is eligible for my project:
I am a strong believer in the utility of local boards.
I am lucky enough to be able to express myself in at least a couple of languages, but I know this is not the case for everyone.
A lot of users post only on the local boards because of a variety of reasons either language or cultural barriers, lack of interest or whatever other reason.
I personally know a lot of very good users (from the Italian sections mainly, for obvious reason) who doesn't post in the international sections.
I think all those users are missing a lot of good contents posted on the international (English) section or on other boards.
If you think you can help here, just visit the thread!



