adamstgBit
Legendary

 Offline Offline
Activity: 1904
Merit: 1038
Trusted Bitcoiner


|
 |
April 27, 2014, 01:47:36 AM |
|
Agreed Adam, but not until the long-running ChinaFUD soap opera concludes.
This may be during May, but only when the global price has adjusted to reflect that CNY transfers to/from the China exchanges are severely and permanently crippled.
for me china is done... there banning it, srota wtv the F that means..... idk why they let that 2 hour bitcoin documentary run on there tv b4 they SORTA banned it. but wtv the rest of the world is cheering for freedom and so am I! |
|
|
|
|
adamstgBit
Legendary

 Offline Offline
Activity: 1904
Merit: 1038
Trusted Bitcoiner


|
 |
April 27, 2014, 01:53:30 AM |
|
free the market free the world bitcoin is gana be the money in the future we all know this.... the network is perfect, and perfection is constantly being improved upon. programmers know murphy's law "everything that can go wrong..." and they have programed that into the fucking code man you know whatn i'm saying. welcome to hollywood 2012 when the bits where free  |
|
|
|
|
dnaleor
Legendary

 Offline Offline
Activity: 1470
Merit: 1000
Want privacy? Use Monero!

|
 |
April 27, 2014, 01:56:01 AM |
|
free the market free the world bitcoin is gana be the money in the future we all know this.... the network is perfect, and perfection is constantly being improved upon. programmers know murphy's law "everything that can go wrong..." and they have programed that into the fucking code man you know whatn i'm saying. welcome to hollywood 2012 when the bits where free  hehe, totally agree  We needed some very needed bullish posts  Same chart, just linear:     |
|
|
|
|
wachtwoord
Legendary

 Offline Offline
Activity: 2338
Merit: 1136

|
 |
April 27, 2014, 01:56:36 AM |
|
Agreed with dnaleor & Adam, but not until the long-running ChinaFUD soap opera concludes.
It will never conclude. Good thing it doesn't really matter. Hopefully, at some point, people will figure this out. |
|
|
|
|
Patel
Legendary

 Offline Offline
Activity: 1320
Merit: 1007


|
 |
April 27, 2014, 02:00:52 AM |
|
Thinking about this always makes me excited.
Atlas, Circle, Coinsetter, SecondMarket Exchange, Xapo, Buttercoin, and some others have raised more than $100 million + combined in investments.
When these companies launch, they are going to have to do some serious marketing to bring volume to their exchanges so they can start earning to break even on their investments.
I think when these guys start their marketing campaigns, the price and volume is going to skyrocket.
|
|
|
|
|
ChartBuddy
Legendary

 Offline Offline
Activity: 2478
Merit: 2092
1CBuddyxy4FerT3hzMmi1Jz48ESzRw1ZzZ

|
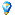 |
April 27, 2014, 02:01:00 AM |
|
|
|
|
|
|
billyjoeallen
Legendary

 Offline Offline
Activity: 1106
Merit: 1007
Hide your women


|
 |
April 27, 2014, 02:05:47 AM |
|
Happy days are here again why exactly? I really want to know. What has changed?
I think it's improbable that China is done fucking the world markets until it shoots its wad right in Bitstamp's butthole. We have at least 3 potential goxxings on our hands because Huobi, BTC China and OK Coin are all sketchy volume-faking exchanges with very limited and diminishing sources of deposits. It doesn't matter if it's their fault or the PBoC or someone else. These exchanges are likely going to wither and die, crash out or go offshore. Markets will be rattled and you can either be in a position to profit, ride out the storm or get caught with your pants down.
China is a 50 ton battleship anchor on BTC price and will continue to be until the chain is broken. That doesn't make me happy, but pretending significant negative factors don't exist makes for poor investment strategy. So if there is something good that outweighs this Chinese clusterfuck, I'd love to hear about it, but don't tell me it isn't real or it's irrelevant.
|
|
|
|
|
chessnut
Legendary

 Offline Offline
Activity: 924
Merit: 1001

|
 |
April 27, 2014, 02:07:04 AM |
|
there comes a point where the market rises unexplained regardless of news. historically, the best time to buy is during genuine tragedy, even (especially) during serious wars. the day will come, when this market will rise regardless of china. something to do with offshore exchanges opening in USA and Europe, I suspect.
|
|
|
|
|
adamstgBit
Legendary

 Offline Offline
Activity: 1904
Merit: 1038
Trusted Bitcoiner


|
 |
April 27, 2014, 02:08:24 AM |
|
poeple we need to forget about 1 billion chinese poeple making us all rich beyond belief and fouces on what really matters making us all rich beyond belief  |
|
|
|
|
aminorex
Legendary

 Offline Offline
Activity: 1596
Merit: 1030
Sine secretum non libertas

|
 |
April 27, 2014, 02:08:36 AM |
|
the distribution of D(i) must satisfy E(exp(D(i)) = Q, not 1; and one can achieve that even with a zero-mean Gaussian if desired. In that case one would have a legitimate log-Browninan model (with Gaussian increments) such that that E(Z(i0+n)) = Z(i0), E(P(i0+n)) = P(i0)*Q^n, and Prob(P(i0+n) < P(i0)) = 1/2. Does this make sense?
That's what all my models do, except I never use gaussians unless I need consistency with closed form options. Can't tell you if it's standard. Regarding EMH, for every Rijksbank prize winner who advocates some formulation, I can name 2 who will repudiate that formulation as obviously inconsistent with basic observations. Use it every day, in order to do principled valuations, but give it no credence. |
|
|
|
|
ElectricMucus
Legendary

 Offline Offline
Activity: 1666
Merit: 1057
Marketing manager - GO MP


|
 |
April 27, 2014, 02:22:03 AM |
|
poeple we need to forget about 1 billion chinese poeple making us all rich beyond belief
and fouces on what really matters
making us all rich beyond belief
Posting will surely accomplish that, right? |
|
|
|
|
adamstgBit
Legendary

 Offline Offline
Activity: 1904
Merit: 1038
Trusted Bitcoiner


|
 |
April 27, 2014, 02:22:44 AM |
|
poeple we need to forget about 1 billion chinese poeple making us all rich beyond belief
and fouces on what really matters
making us all rich beyond belief
Posting will surely accomplish that, right? lol! i banking on the youngsters doing a good job i'm getting old guys....    |
|
|
|
|
podyx
Legendary

 Offline Offline
Activity: 2338
Merit: 1035

|
 |
April 27, 2014, 02:41:50 AM |
|
I just wanna feel the moment of the next bull run
|
|
|
|
|
|
Nightowlace
|
 |
April 27, 2014, 02:50:55 AM |
|
I just wanna feel the moment of the next bull run
It's very very very long overdue |
|
|
|
|
gentlemand
Legendary

 Offline Offline
Activity: 2604
Merit: 3056
Welt Am Draht

|
 |
April 27, 2014, 02:56:49 AM |
|
The feeling of a price explosion has almost slipped my mind. Much has changed since the last one. I'm guessing it'll take a big dollop of US inspiration to get the next one rolling.
|
|
|
|
|
podyx
Legendary

 Offline Offline
Activity: 2338
Merit: 1035

|
 |
April 27, 2014, 02:59:07 AM |
|
The only thing that makes me doubt $7k bubble this summer/autumn is that this is the big one
this is gonna be the one who makes or break bitcoin
|
|
|
|
|
adamstgBit
Legendary

 Offline Offline
Activity: 1904
Merit: 1038
Trusted Bitcoiner


|
 |
April 27, 2014, 02:59:15 AM |
|
The feeling of a price explosion has almost slipped my mind. Much has changed since the last one. I'm guessing it'll take a big dollop of US inspiration to get the next one rolling.
its turning around now really... |
|
|
|
|
ChartBuddy
Legendary

 Offline Offline
Activity: 2478
Merit: 2092
1CBuddyxy4FerT3hzMmi1Jz48ESzRw1ZzZ

|
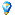 |
April 27, 2014, 03:01:09 AM |
|
|
|
|
|
|
JayJuanGee
Legendary

 Online Online
Activity: 4018
Merit: 11833
Self-Custody is a right. Say no to "non-custodial"

|
 |
April 27, 2014, 03:04:21 AM |
|
Happy days are here again why exactly? I really want to know. What has changed?
I think it's improbable that China is done fucking the world markets until it shoots its wad right in Bitstamp's butthole. We have at least 3 potential goxxings on our hands because Huobi, BTC China and OK Coin are all sketchy volume-faking exchanges with very limited and diminishing sources of deposits. It doesn't matter if it's their fault or the PBoC or someone else. These exchanges are likely going to wither and die, crash out or go offshore. Markets will be rattled and you can either be in a position to profit, ride out the storm or get caught with your pants down.
China is a 50 ton battleship anchor on BTC price and will continue to be until the chain is broken. That doesn't make me happy, but pretending significant negative factors don't exist makes for poor investment strategy. So if there is something good that outweighs this Chinese clusterfuck, I'd love to hear about it, but don't tell me it isn't real or it's irrelevant.
So, if you were a betting man, you would be siding with Windjc about the $435 in the next 30 days? or do you believe the downfall and FUD spreading of china is gonna last longer than 30 days? I agree with you that China remains a relevant factor.. and will continue to be a relevant factor, until some other more relevant factor drowns it out.. such as major investment entering into the market (pie in the sky? does NOT seem to be a long shot)...The existence of these three Fud-spreading China exchanges does seem rife for some kind of a GOX-like scandal, though. |
|
|
|
|
|
octaft
|
 |
April 27, 2014, 03:40:05 AM |
|
The only thing that makes me doubt $7k bubble this summer/autumn is that this is the big one
this is gonna be the one who makes or break bitcoin
Why do people equate the success of bitcoin with the price of bitcoin? |
|
|
|
|
|




 Poll
Poll
