tromp
Legendary

 Offline Offline
Activity: 978
Merit: 1077

|
 |
November 16, 2015, 06:41:47 PM |
|
This means that in average computation of a single bit takes less time than computation of the whole hash.
Like I said it takes a about a percent less. All that article does is propose an extremely inefficient way of evaluating SHA256, as some of the comments there already point out. You should find more reputable sources to support your questionable claims. |
|
|
|
|
|
|
|
Even in the event that an attacker gains more than 50% of the network's
computational power, only transactions sent by the attacker could be
reversed or double-spent. The network would not be destroyed.
|
|
|
Advertised sites are not endorsed by the Bitcoin Forum. They may be unsafe, untrustworthy, or illegal in your jurisdiction.
|
|
|
|
|
Come-from-Beyond (OP)
Legendary

 Offline Offline
Activity: 2142
Merit: 1009
Newbie

|
 |
November 16, 2015, 06:47:36 PM |
|
Here's one: Argon2, winner of the Password Hashing Competition.
Argon2 whitepaper says that time-memory trade-off still can be used. At some point the trade-off stops working because computational units will occupy more space than the removed memory but this protection won't work for a quantum computer with its perfect parallelism of computations. Looks like Argon2 fails to deliver protection against quantum computers. |
|
|
|
|
|
|
tromp
Legendary

 Offline Offline
Activity: 978
Merit: 1077

|
 |
November 16, 2015, 07:07:40 PM |
|
Here's one: Argon2, winner of the Password Hashing Competition.
Argon2 whitepaper says that time-memory trade-off still can be used. At some point the trade-off stops working because computational units will occupy more space than the removed memory but this protection won't work for a quantum computer with its perfect parallelism of computations. Looks like Argon2 fails to deliver protection against quantum computers. The whitepaper (Table 1) says that reducing memory for Argon2d by a mere factor of 7 requires increasing the amount of computation by 2^18, and it only gets much worse beyond that. Best of luck with your perfect quantum computer. |
|
|
|
|
Come-from-Beyond (OP)
Legendary

 Offline Offline
Activity: 2142
Merit: 1009
Newbie

|
 |
November 16, 2015, 07:14:51 PM |
|
The whitepaper (Table 1) says that reducing memory for Argon2d by a mere factor of 7 requires increasing the amount of computation by 2^18, and it only gets much worse beyond that.
Best of luck with your perfect quantum computer.
So it requires to add 18 qubits to that perfect quantum computer, it seems? Have you seen this pic: 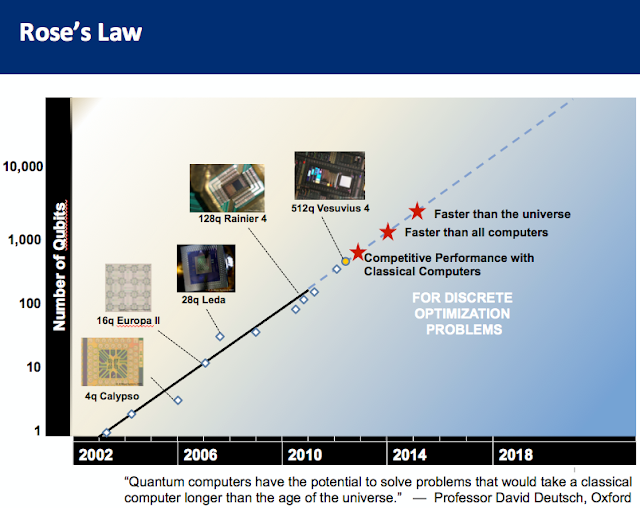 |
|
|
|
|
|
WorldCoiner
|
 |
November 16, 2015, 08:51:02 PM |
|
Two years ago I was the first German blogger that took notice of Nxt. I hope for IOTA I can also play an important role to create attention in the German speaking communities (what includes Switzerland and Austria as well). This first post includes a lot of information from this thread also some parts of the cointelegraph interview and other sources from the web. In addition I brought attention to Jinn and how IOTA is related to this semiconductor start up: https://altcoinspekulant.wordpress.com/2015/11/15/iota-kryptowaehrungsrevolution-zum-internet-of-things/Have a good start in the week! Thanks a lot ! Of course David. It would be great if I could contact you as well for an interview, not right now but begin of December, when we get closer to the ICO date. Just 4-5 questions. Many thanks in advance! |
|
|
|
|
tromp
Legendary

 Offline Offline
Activity: 978
Merit: 1077

|
 |
November 16, 2015, 09:01:57 PM |
|
The whitepaper (Table 1) says that reducing memory for Argon2d by a mere factor of 7 requires increasing the amount of computation by 2^18, and it only gets much worse beyond that.
Best of luck with your perfect quantum computer.
So it requires to add 18 qubits to that perfect quantum computer, it seems? You are rather confused about the abilities of quantum computers. A 2^18 increase in sequential computation is also a 2^18 increase in quantum runtime. Please read http://www.cs.virginia.edu/~robins/The_Limits_of_Quantum_Computers.pdfto understand what quantum computers can and cannot do. Scott also writes regularly about DWave and their snake-oil version of quantum computer that your pictures alludes to. See http://www.scottaaronson.com/blog/?p=2448 |
|
|
|
|
Come-from-Beyond (OP)
Legendary

 Offline Offline
Activity: 2142
Merit: 1009
Newbie

|
 |
November 16, 2015, 09:11:47 PM |
|
DWave is not a quantum computer, that's true. Regarding that 2^18 issue, your paper says: A small number of particles in superposition
states can carry an enormous amount of information:
a mere 1,000 particles can be in a superposition
that represents every number from 1 to
2^1,000 (about 10^300), and a quantum computer
would manipulate all those numbers in
parallel, for instance, by hitting the particles
with laser pulses. While it's obvious that 1 number is not enough for Argon2 computation, if we assume that 10 numbers is enough then 18*10 extra qubits should solve the problem. Right? |
|
|
|
|
|
|
Come-from-Beyond (OP)
Legendary

 Offline Offline
Activity: 2142
Merit: 1009
Newbie

|
 |
November 16, 2015, 09:42:05 PM |
|
An idea has come to my mind. We could use a quantum computer to check SHA256 digests for different patterns by using Kuperberg's quantum sieve algorithm, this would let us to assess how secure SHA256 is. No patterns = hash function is close to random oracle. We could do the same for any algorithm even if it requires petabytes of RAM, we need only digests.
|
|
|
|
|
tobeaj2mer01
Legendary

 Offline Offline
Activity: 1098
Merit: 1000
Angel investor.

|
 |
November 17, 2015, 04:20:16 AM |
|
What algorithm will IOTA use, can I mine it?
|
Sirx: SQyHJdSRPk5WyvQ5rJpwDUHrLVSvK2ffFa
|
|
|
Come-from-Beyond (OP)
Legendary

 Offline Offline
Activity: 2142
Merit: 1009
Newbie

|
 |
November 17, 2015, 08:29:52 AM |
|
What algorithm will IOTA use, can I mine it?
Iota is not mineable. |
|
|
|
|
|
|
|
|
|
iotatoken
|
 |
November 17, 2015, 02:31:14 PM |
|
Could you rephrase the question? Are you wondering why we did the Tangle instead of Blockchain? |
|
|
|
|
mthcl
|
 |
November 17, 2015, 02:38:12 PM |
|
Sergue, have you ever worked on engineering bio-weapons?
No, that's another guy with the same name. If you continue searching, you'll find a famous violinist as well - that's not me.  |
|
|
|
|
yassin54
Legendary

 Offline Offline
Activity: 1540
Merit: 1000

|
 |
November 17, 2015, 02:52:16 PM |
|
|
|
|
|
|
|
WorldCoiner
|
 |
November 17, 2015, 03:00:16 PM |
|
Nice work David, I like graphical work. Also the logo of IOTA is really great. It’s not just about tech in Cryptos, even things like a nice Logo can help to get attention. |
|
|
|
|
Hueristic
Legendary

 Offline Offline
Activity: 3794
Merit: 4874
Doomed to see the future and unable to prevent it

|
 |
November 17, 2015, 03:39:24 PM |
|
Sergue, have you ever worked on engineering bio-weapons?
No, that's another guy with the same name. If you continue searching, you'll find a famous violinist as well - that's not me.  Thx, Could you link your academic background please? Could you rephrase the question? Are you wondering why we did the Tangle instead of Blockchain? I am wondering why the need to replace the blockchain at this time. I am not sold on the idea that yet another coin (token ATM) needs to be created in order to solve the only serious issue I see with current solutions. I am also wondering if current solutions can be upgraded to this tangle with a fork? I understand that alot of work has obviously been put into this effort but I can see a few other methods to monetize this than the creation of yet another coin. Why not propose to the larger Alt projects they morph into this tangle for a fee and use them as a testbed to prove to bitcoin that this would be a hard fork worth pushing. If this were accomplished I see the funding flowing and the infrastructure will not have to be built from the ground up. I am still trying to digest the whitepaper (the math is beyond me) so could you list the bullet points for the advantage/disadvantages v/s blockchain tech. Also that one needs to check in order to �nd a suitable hash for issuing a transaction
is not so huge, it is only around 3
8
. The gain of e�ciency for an \ideal" quantum
computer would be therefore of order 3
4
= 81, which is already quite acceptable (also,
remember that �(
p
N
) could easily mean 10
p
N
or so). Also, the algorithm is such
that the time to �nd a nonce is not much larger than the time needed for other tasks
necessary to issue a transaction, and the latter part is much more resistant agains
quantum computing.
Therefore, the above discussion suggests that the tangle provides a much better
protection against an adversary with a quantum computer compared to the (Bitcoin)
blockchain Saying the time is not much larger is not quantitative. Bloat and TTC are subjective. I'm glad you added the qualifier "Suggests" as I do not see it proven but like I said I cannot follow the math, that is for smarter people than me.  Typo in red. Goddamn I hate quoting from PDF's why do you people continue to use them? Stinking browser plugin failed and I lost all those tabs in the window with the PDF. PDF's are unsafe. ANYTHING ADOBE IS UNSAFE!!!! I finish redoing this later as I have to flush the cache and remove this browser from memory to recover stability and I have pages to backup before that. |
“Bad men need nothing more to compass their ends, than that good men should look on and do nothing.”
|
|
|
|
mthcl
|
 |
November 17, 2015, 03:49:42 PM |
|
|
|
|
|
|
|




